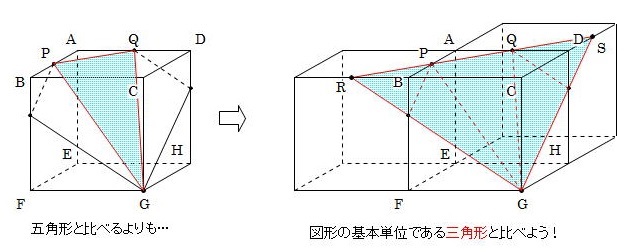
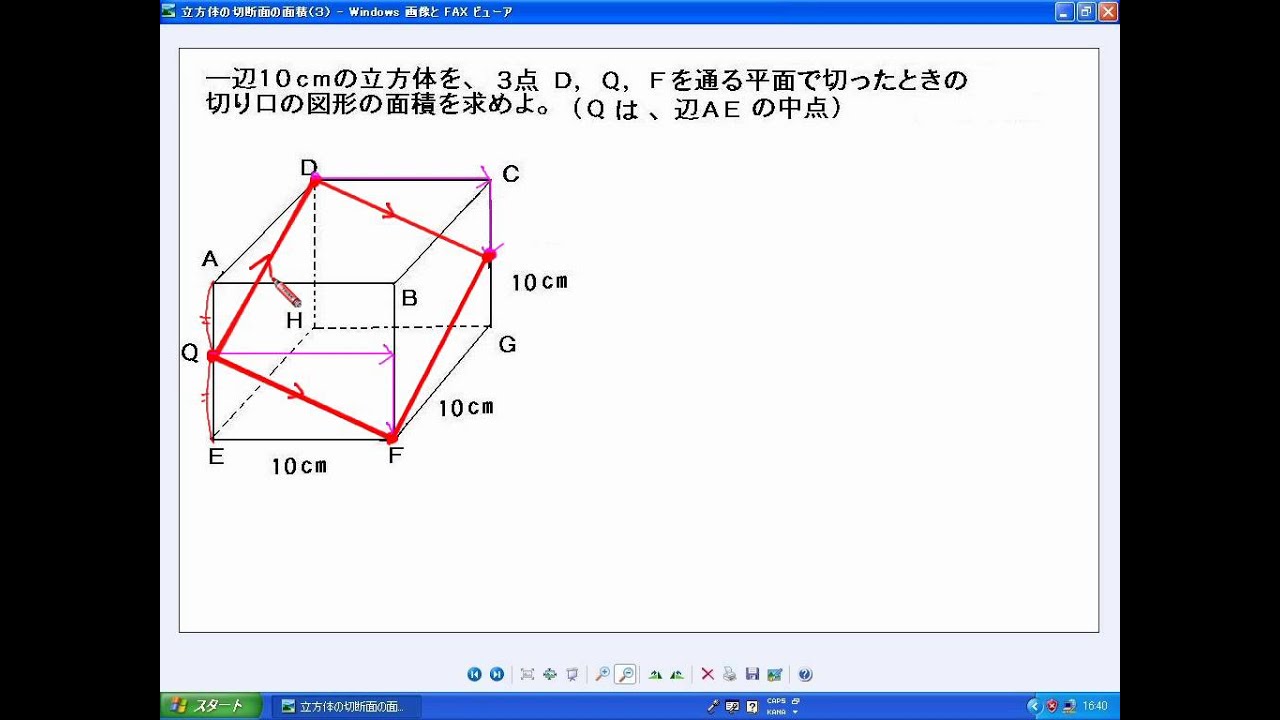
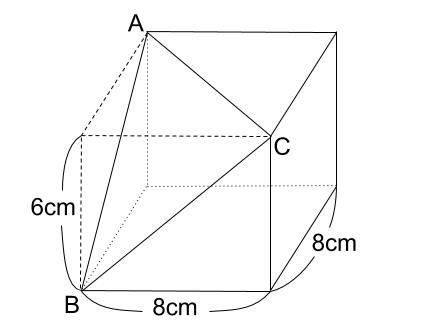
次のように切断面ができる。 m―o―pの線は,最短距離となるように引かれる。 したがって,図に書くと,次のようになる。 em=√(1636)=√52 より,om=√52/3 同様に,pl=√52/3 lm=2√2 oe=pe=(2√52)/3 四角形oplmと eopに分けて考える。 op=4√2 ・四角形oplmビデオ 立方体の切断面 問題集の解説 21, 八月 問題は解析幾何学に関するものです。 これは、ベクトル代数を使用するのと同様に、空間的な線と平面の方程式、立方体の概念とその幾何学的性質を使用して解かれます。切り口の EBDの各辺の長さは、それぞれ 「三平方の定理」 で求められることがわかるかな? そして、「3辺の長さ」が分かったら? 「3辺の長さ」 から 「面積」 を求める方法なら、もう知っているよね。 そう、 「余弦定理でcos」 、 「三角比の公式でsin」 、そして 「面積の公式」 だよね。 こうしてやれば、一見何の関係もないように見える 「直方体の辺の長さ

立方体の切断 面 上の3点を通る平面による 数学カフェjr
立方体 切断面 面積
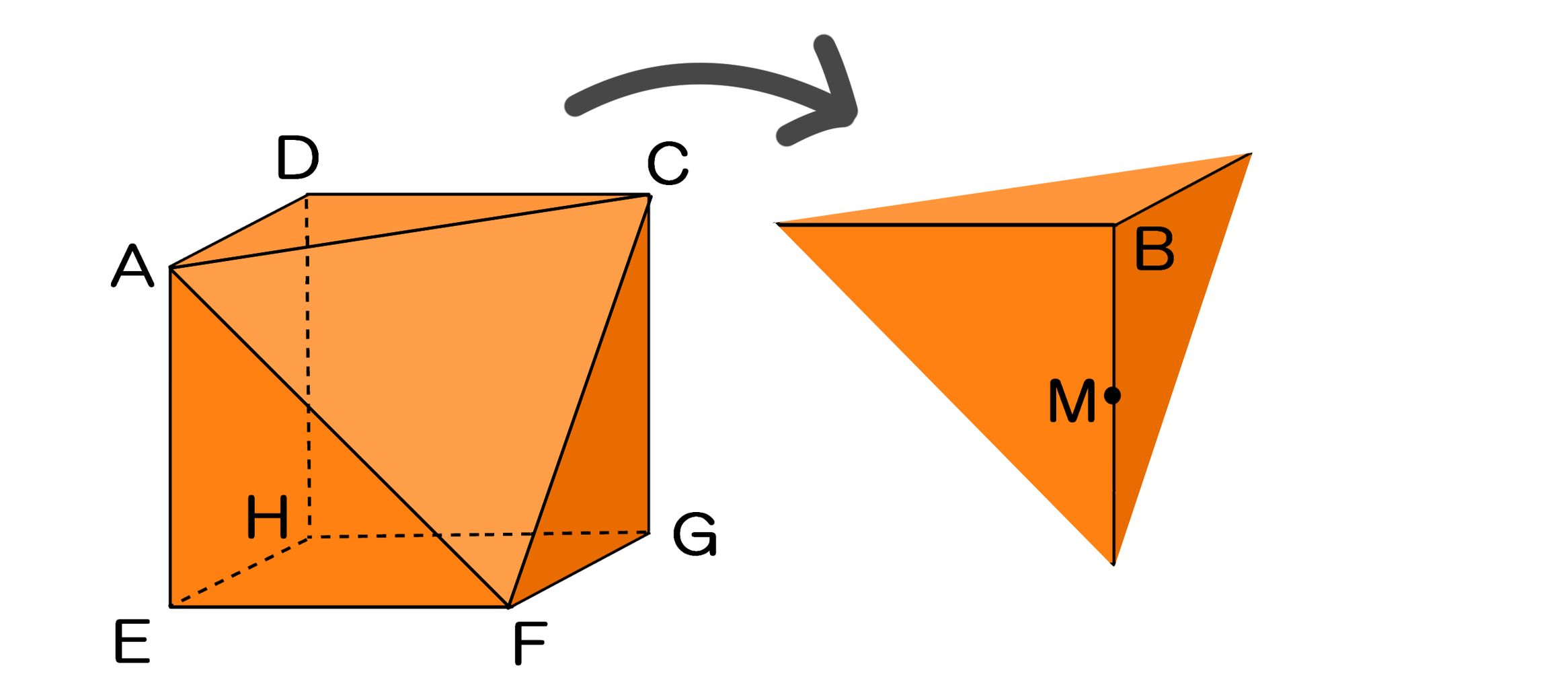
立方体 切断面 面積- 上右図は、切り口を1つの面とする三角錐を抜き書きしたものです。 この三角錐は、点Oで3本の直線が直交(90°で交わる)しています。 次ページ以降、複雑な問題を解説します。 そうした問題の多くで基本となるのが、 点Oで3本の直線が直交する三角錐 です。 この三角錐を適切に作図できれば、立方体の切断面を作図する問題も恐れるに足りません。 と立方体の切断面を作図する問題では、 「立方体の同一面上にある点を結ぶ」 という大原則がまずは重要です。 しかし、この大原則で処理できない点が存在する場合、ここまでで見てきたように、 三角錐を作る方法 が有効です。 三角錐を作る際には、 3本の直線が直交する点Oの位置を正確に定めてくださいね(最後の超難問では、直交し



立体の切断
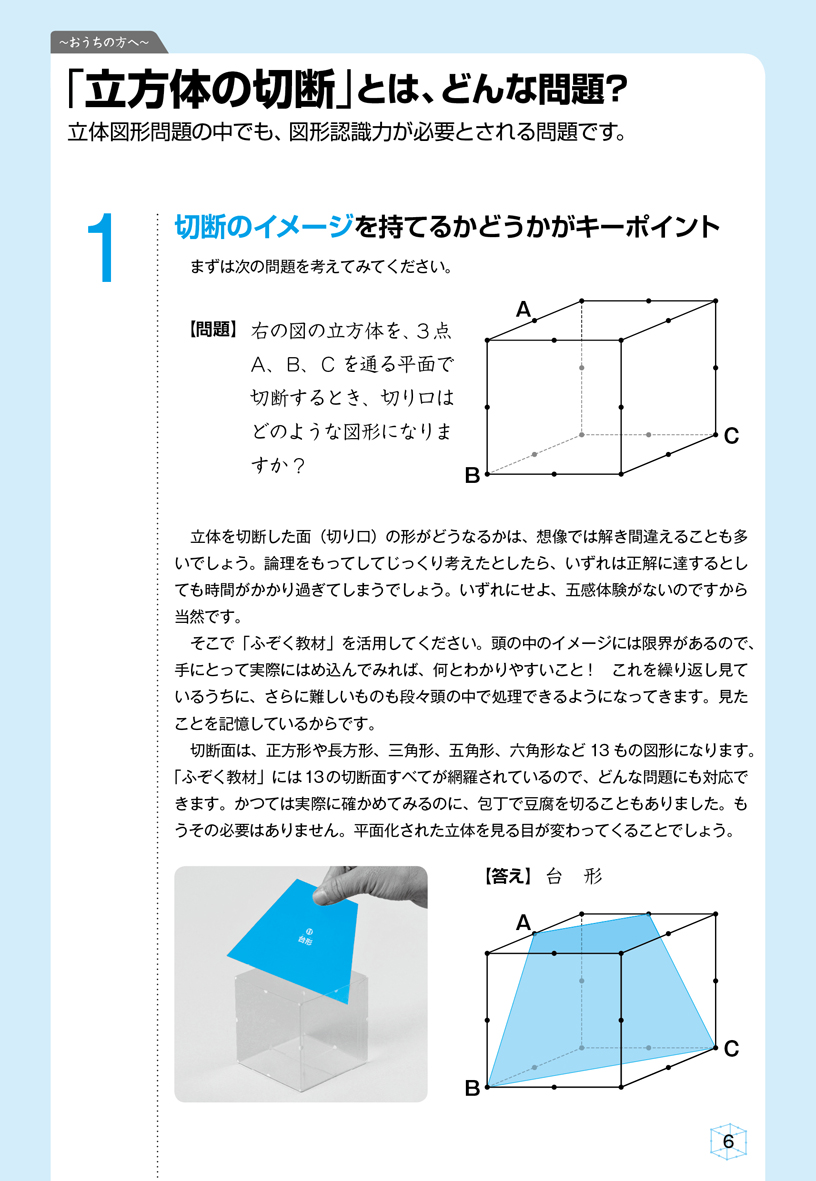
1 同じ面にある2点を結ぶ(結べる)! 問題)下記の立方体をA、C、Fを通る平面で切断した切り口を作図してください 出典:『塾技100算数』p104 図の通りですね。 同じ面にある2点を結ぶ(結べる)! 2 向かい合う面(平行な面)の切り口は必ず平行になる! 立方体を切った時にできる切断面の寸法を公開します。 100均ショップの透明プラスチック容器に入れれば、「あの教材」と同じ体験ができます。 前提にした立方体の寸法 使用する透明プラスチック容器は、これです。 うち のりを ノギスで測ってみたら開口は573mmありました。 今回の切断面の形を見るための型紙は一辺を56mmとして設計しました 青の三角形の面積は、8×8-(8×4÷2×2+4×4÷2)=24㎝2 青の三角形の部分の相似比が1:2なので、面積比が1:4になることから、黒斜線部の面積は青の三角形の3/4。 よって、24×3/4=18 ㎝2 算数って楽しいわぁ♪
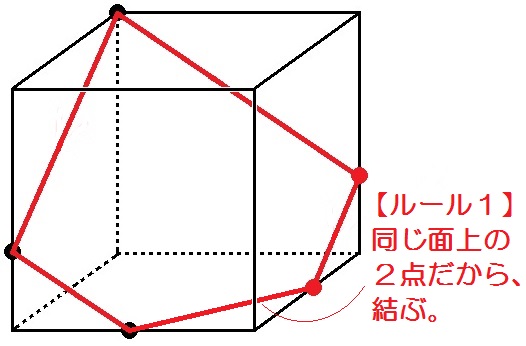
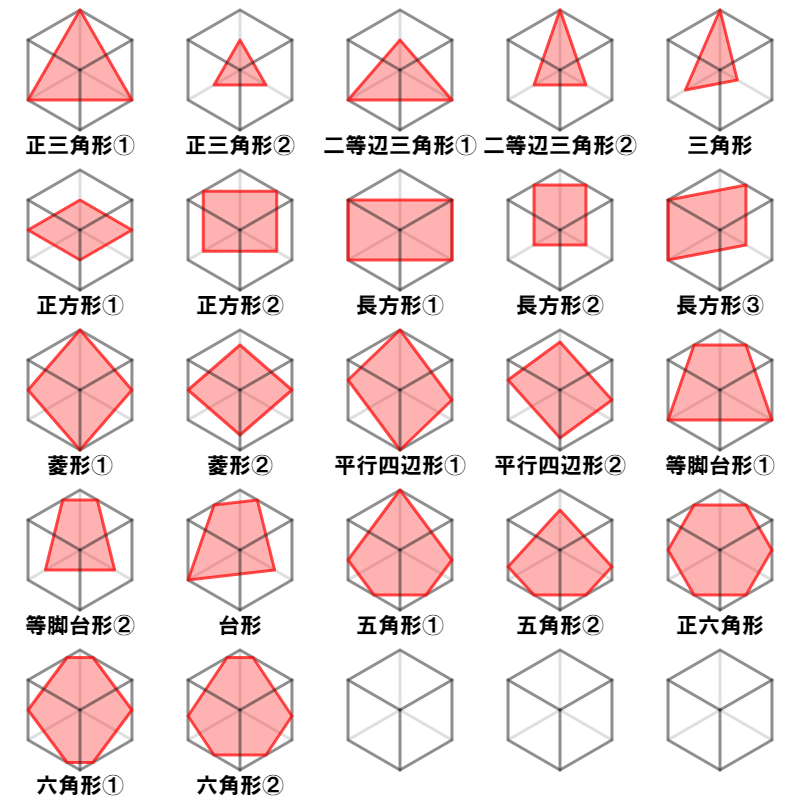
この3つで、切断面がどのような形になるのかを見分けることが出来ます。 切断面がわからず悩んでいるお子さんの大半は、これで解決します。 具体的に下の図のような立方体で説明します。 (1) 頂点BDGを通る平面で切断。 頂点BD、頂点BG、頂点DGはそれぞれ同じ面にあるので、線で結びます。 図のように、切り口は正三角形となります。 (全ての辺の長さ 立方体の切断「①立方体の同一平面上にある2点を直線で結ぶ」「立方体の切断面の面積が展開図から求まることがある1」 13 ワンセンテンス算数 21年3月28日 0923 ¥100 オンライン家庭教師やってい立方体では, 向かい合う面どうしは平行だ 平行な面に現れる切り口の線は平行になる ルール ③ 「 一直線の法則 」: 切断面は横から見ると一直線 お豆腐という名の立方体を包丁という名の平面で切って
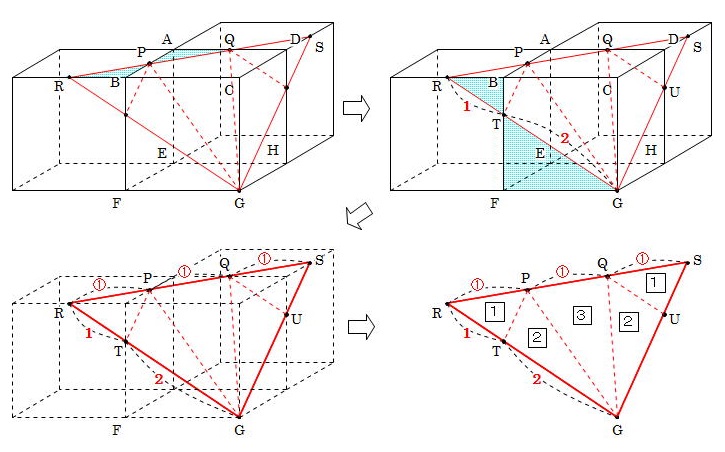
さて、これで切断面が作図できましたから、何を求めるかもわかります。 できあがった切断面は五角形ですから のように、作図の際に延長したことが役立つように親切な作問がなされています。 ここまでくれば、 となり、 切断面の面積は 232=7、図のような一辺の長さが1の立方体があり 3点0a,0,0 ,1 00,a,0,1 00,0,a1を通る平面で 切断したときの切断面の面積をS0 1a とする。 S0 1a をaで表し最大値を求めよ。 i)0(a(1のとき S0 1a = 1 2 ・0 1U2a 2sin60,= U3 2 a2 )1(a(1) 立体acfhは4つの面で囲まれた多面体である。 三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。




立方体の切断 切断面の寸法を公開します 駒澤塾 中学受験の算数 理科




三平方の定理の利用 Ict教材eboard イーボード
それらを立方体の頂点同士を結ぶ直線の中で最も長い一本に重なるように組み合わせれば、隙間無くぴったりと立方体を満たします。 立方体 切断キット04 まったく同一の四角すいが3個です。 この四角すい、底面積は元の立方体の一つの面と同一の正方形よって、 AP A P の長さは、立方体の対角線 AG A G の 3 32 3 3 2 です。 1 1 辺が 4cm 4 c m の立方体の対角線の長さは 4√3 4 3 なので AP = 4√3× 3 32 = 12√3 5 A P = 4 3 × 3 3 2 = 12 3 5 と求まります。 スポンサーリンク 立方体の切断に関する問題が表裏形式で11題ならんでいます。 11題のうち3題は実際の入試問題(大谷中、昭和学院秀英中、城北中)を一部改変したものです。 問題の内容 ★切断面の形から見取り図に切断線を書き込む



14年度 中学入試分析11 切断面の面積比 前田昌宏の中学受験が楽しくなる算数塾



切断した立体の表面積は サレジオ学院中学 2014年 どう解く 中学受験算数
立方体の切断 切断面が五角形になるパターン(立体の角出し) 表面積の差を求める その他の形状になる切断 芝浦工大 大問1(9) 立方体の面の中央を通る切断 正八面体の体積 立方体以外の切断 三角錐の切断 立教新座 大問3 三角錐の切断About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creatorsで,abcd と比べると面積は 2 1 である。 すなわち,abcd の面積を s とすると,efgh の面積は s 2 1 になる。 この正四角錐と立方体の高さは共通であるので,ともに h と表すことができる。 (立方体の体積)=(底面積)×(高さ)= sh (正四角錐の体積)= 3 1 ×(底



Math 空間図形 立体の切断と切り口 働きアリ The 2nd



立方体を図のように頂点a Cと辺の中点b Dで切断すると 切断面ab Yahoo 知恵袋
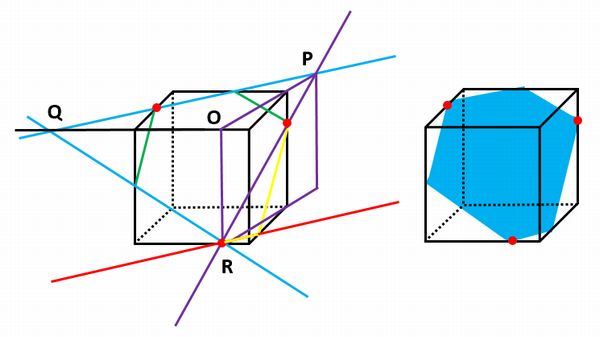
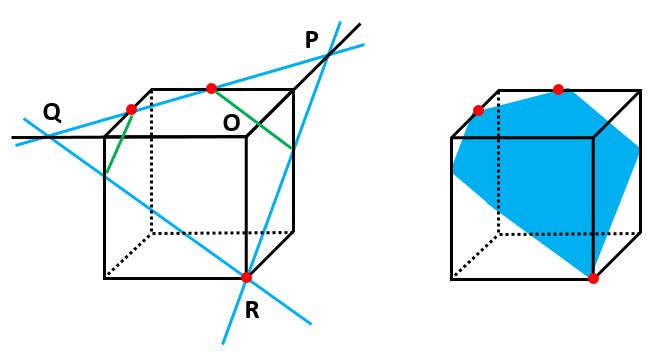
切り口が六角形になる場合の作図 この問では、単純に3点を結んではいけません。 前ページの大原則(立方体の同一面上にある点を結ぶ)に従って、底面の2点だけを結びます。 2点を結んだ線分を両側に延長します。 この延長した直線と同一平面で交わるように、立方体の辺も延長します。 それぞれの直線の交点を下図の通りP,Qとします。 Pと同一平面上にある点立方体の切断基礎編1 ここでの問題は 「立方体の辺上にある3つの点を通る平面で立方体を切断すると,切り口の 形はどんな形になるだろうか?」 というものです。 基礎知識 1 3点を通る平面はただ1つに決まる。 前提1 A~Hは立方体の頂点。 立方体の積木の場合、表面積は「3方向の面積の和×2 」で求められますが、凹みがある場合は少し注意が必要です。 投影図(推理) 投影図から得られる情報は完全ではないことがあります。



バカでもわかる 中学数学



空間図形 立方体の切断面を作図する 切り口の多角形はどんな形 ページ 4 みみずく戦略室
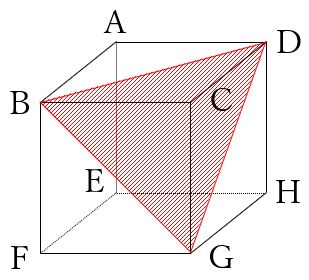
立方体のののの切断面切断面 京都大年ほか多数 三角形と六角形が現れる状況が理解できても面積を求めることは,また別の困難さを伴う作 業です。新課程では空間での平面方程式や直線の扱いが削除されたが,本問は数学bの空間立方体の断面の面積 三平方の定理を使い、立方体の断面の面積を求めてみましょう。 1辺が5cmの立方体があります。 断面ABCDの面積を求めてください。 1. 1辺が10cmの立方体があります。 断面ABCの面積を求めてください。 2. 1辺が10cmの立方体があります。 断面ABCの面積を求めてください。 点A、B、C は1辺の中点です。 3点を通る平面でこの立方体を切断する。 aq=9, ap=15のとき次の問いに答えよ。 四面体aepqの体積を求めよ。 epqの面積を求めよ。 頂点aから面epq




数学の問題です 一辺の長さが2の立方体abcdefghの辺ab 辺ad Okwave



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ
切断面sの面積を次の式で求めます。 s=正方形の面積―(s1+s2+s3) で求めることができるよ。 つまり、立方体の体積は、 1辺×1辺×1辺 中学受験生が苦手とする空間図形分野のうち、立方体の切断面を作図する問題を解説します。1辺の長さが4cmの立方体を切断してできる立体について, (1) 点Fを含む方の立体の表面積 解 右図参照(2等分に切断) 切り口はひし形AJGIで,IJ=4√ 2 ,AG=4√ 3 表面積=(立方体の表面積)÷2+ひし形 =4 2 ×6÷2+(4√ 2 ×4√ 3)÷2 = 48+8√ 6 cm 219年 5年生 6年生 入試解説 東京 男子校 立体の切断 麻布 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用




立方体の切断の問題 16年本郷中 元オカマの家庭教師の独り言
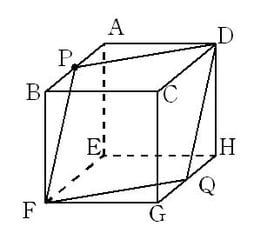



立方体 切断 展開図 解説 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
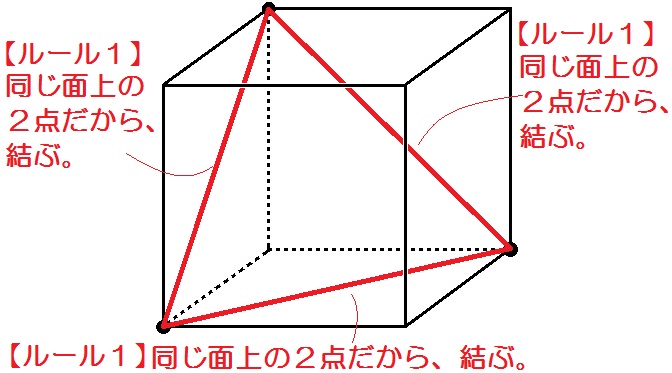
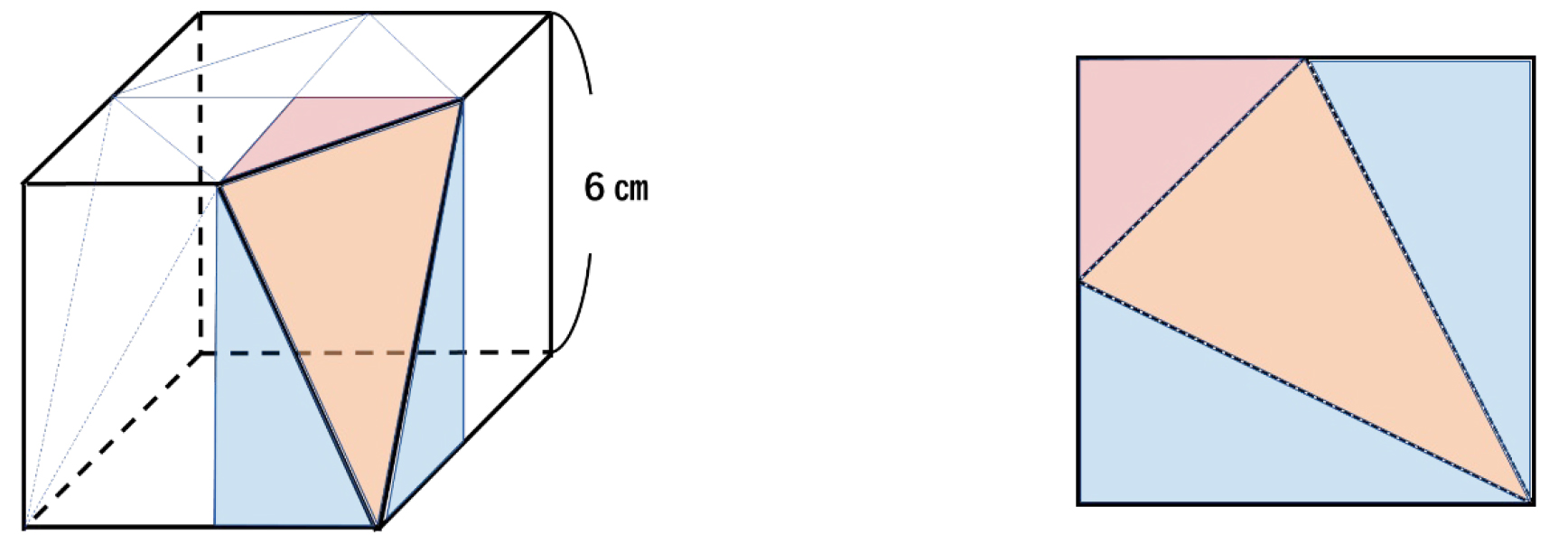
同じ面にある2点を結ぶ 立体切断の問題は、「立方体の辺上にある3つの点を通る平面で切断する」というものになります。 まずは、3つの点のうち2つが同じ面の上にあるか探し、その2点を結びましょう。 上の図のように、 立方体には6つの面があるので、そのいずれかの上で2点を結ぶことができることがほとんど です。 最初に引いたこの直線をもとにして、切断この立方体 を, 4つの点 P, Q, F, Hを通る平面で2つに切り分けまし た。 (1) 2つに切り分けた立体の表面積の差は何 です か。 (2) 頂点Cをふくむ立体の体積は何 です か。 全部で正方形の面積が5 つ分となることがわかると思います。 立方体の1 辺の長さが6㎝だとすると、表面積は 6 ㎝×6 ㎝×5= 180 ㎠ であることがわかります。 立体の切断にも登場② 立体の切断の問題でよく見る切断の形です。
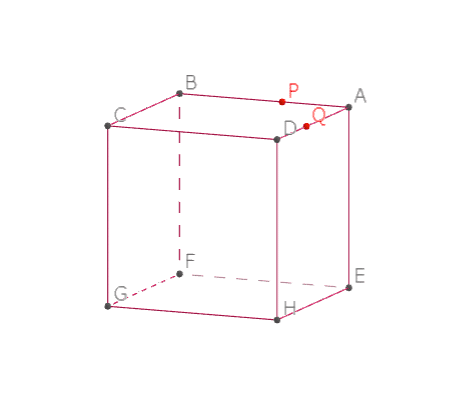



立方体の切断 切断面が5角形の時の体積は 断頭四角柱の体積を利用してだすこともできる ワンセンテンス算数 Note
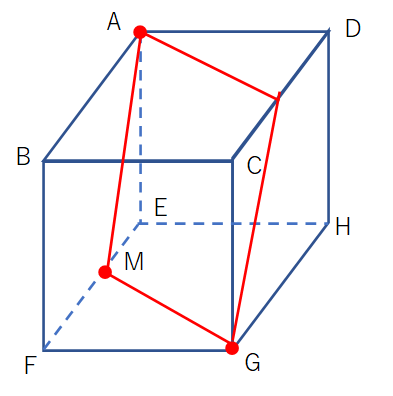



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ



一辺の長さが4の立方体abcd Efghに内接する球がある この球を Yahoo 知恵袋
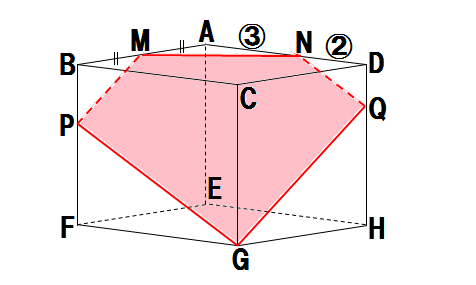



345 立方体の切り口 問題集




立体の切り口の面積 中学3年数学 Youtube



年 東京消防庁 類2回目 14 切断面 空間把握 西川マキ 公務員試験 数的処理 就職試験 Spi 講師 Note




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




立方体の切断 に関するまとめをアップしました お見逃しなく 恋する中高一貫校 適性検査 徹底攻略




06 号 立体パズルおよび型枠 Astamuse




切断面のある立体の表面積 算数の問題 身勝手な主張



楽天ブックス 立方体の切断の攻略 本



Docs Wixstatic Com Ugd f912 98fb61e4a43baa0d3d93a7f7ce5 Pdf Index True



1 4 Cm Abcdefgh Bf P Descubre Como Resolverlo En Qanda



立体の切り口 中学受験ー算数解き方ポータル



14年度 中学入試分析11 切断面の面積比 前田昌宏の中学受験が楽しくなる算数塾



立体切断 その4 中学受験算数の家庭学習教材 カンガループリント




立方体の切断の攻略 受験脳を作る 村上綾一 村上綾一 本 通販 Amazon




立体内部の1点 を通る平面による 立方体の切断 城北 数学カフェjr
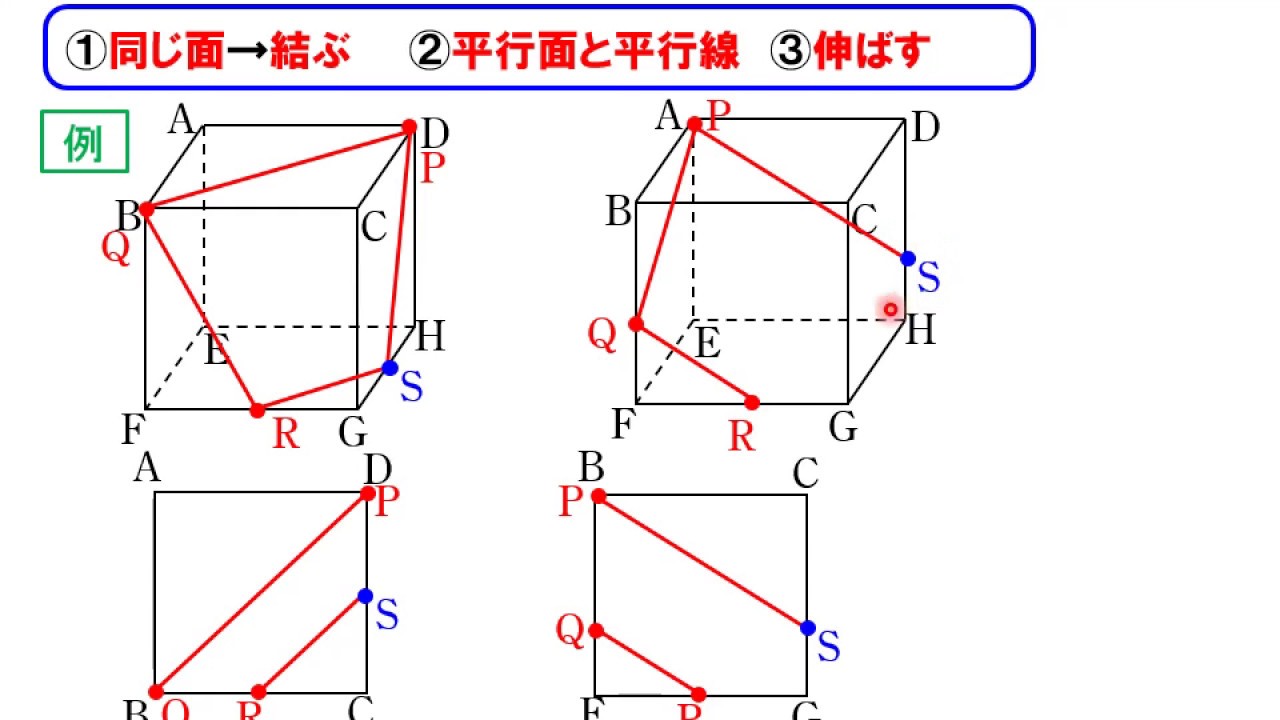



空間図形01 立方体の切断1 Youtube



三石 数学塾 立方体の切り口 その1
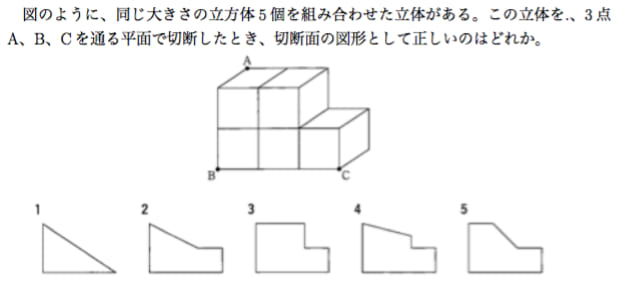



5つの立方体 切断 切断面の形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




立方体の切断 面 上の3点を通る平面による 数学カフェjr




発展 三角比と直方体 なかけんの数学ノート




高校数学 直方体の切り口の面積 例題編 映像授業のtry It トライイット



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Rippoutai Cut0001 Pdf




第10回 立体図形必勝法 立方体の複数切断 算数ドクター




よく見かけますね この展開図 後編 中学受験プロ講師ブログ




天才いますか 教えてください Af Cfの線は気にしないでくださいw Clear




21年 甲陽学院中 算数 第一日 問3 立体の切断面の面積比
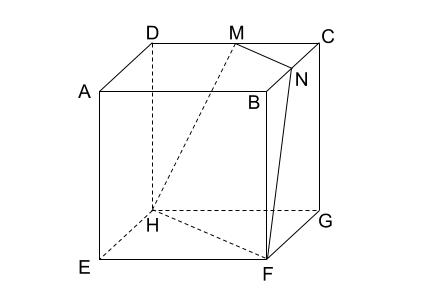



立方体の切断面の頂点からの距離 中学数学の無料オンライン学習サイトchu Su
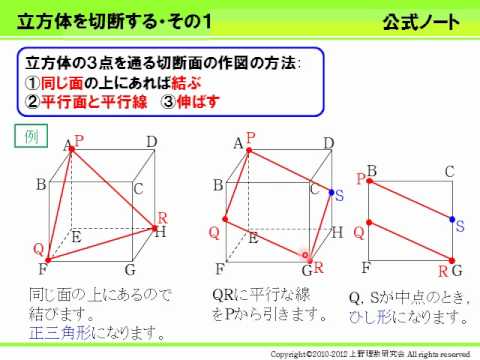



立方体の切断1 Youtube



立体の切り口問題より 切断面の面積 栄東中学東大選抜 2009年 これが中学入試に出た図形問題




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




立方体の切断 基本の切断 駒澤塾 中学受験の算数 理科



切断面の面積です 次の図のような1辺が2aの立方体を A B Cの3 Yahoo 知恵袋




レベル別解説 レベル選択アドバイス 中高一貫コース 通信教育 中学生 中学生 z会




公務員の空間把握の問題で解説みても理解できなお願い Okwave



Http Www Min San Com Pd Z5 41 2 Kai




Cube Taraognn



3



1



立体の切断の問題 教えてほしい問題があります 問題 下の図で3点 Yahoo 知恵袋



湘南白百合11 5 立体図形 立方体を切断してできる立体の体積や表面積 気まぐれ解説カフェ 仮



空間図形 立方体の切断面を作図する 切り口の多角形はどんな形 ページ 3 みみずく戦略室




問題174 立方体に潜む正多角形



立体切断の3つの基本 中学受験プロ講師ブログ



切り口の面積比は 今年 2019年 麻布中学 どう解く 中学受験算数



中学数学 空間図形 立体の切断問題のコツ



立方体の切り口の面積 3 Youtube



中学数学 空間図形 立体の切断問題のコツ



立体の切断




問題114 立体の切断




立方体の切り口の面積 2 Youtube



From灘 立方体の切り口は 朝日小学生新聞 中学受験eye 関西圏




立方体の切断の問題 16年本郷中 元オカマの家庭教師の独り言
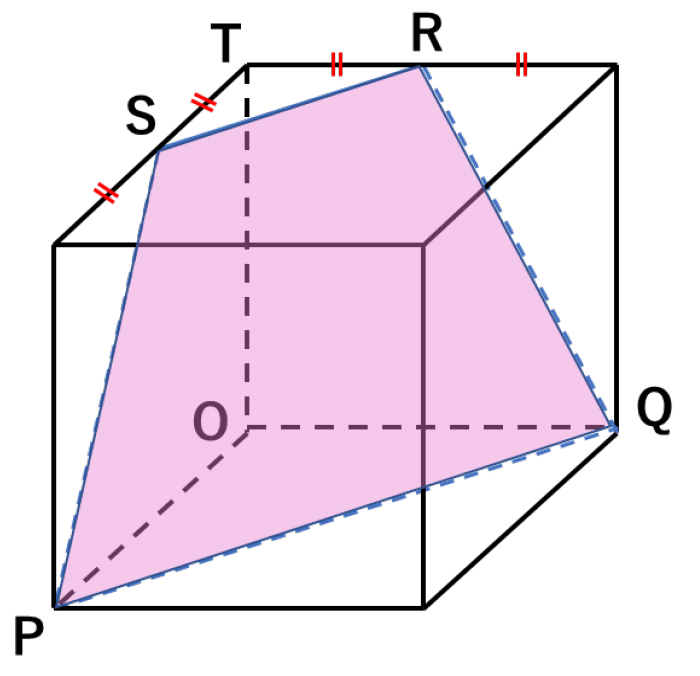



よく見かけますね この展開図 後編 中学受験プロ講師ブログ




中1 20 5 立方体の切断と体積 Youtube



14年度 中学入試分析11 切断面の面積比 前田昌宏の中学受験が楽しくなる算数塾



Studydoctor立体の切り口の面積 中学3年数学 Studydoctor



Math 空間図形 立体の切断と切り口 働きアリ The 2nd



立体の切断面の作図方法1 をアップ 久保塾 今治市の学習塾




空間の切断面の面積を求める問題 無料で使える中学学習プリント




中学数学 空間図形
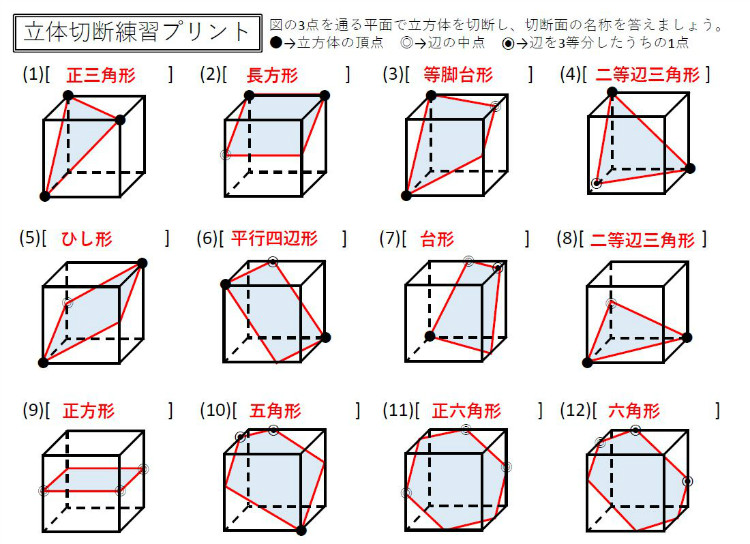



講義内容3



図は1辺6cmの立方体であるこの立方体を頂点a F Cを通る平 Yahoo 知恵袋
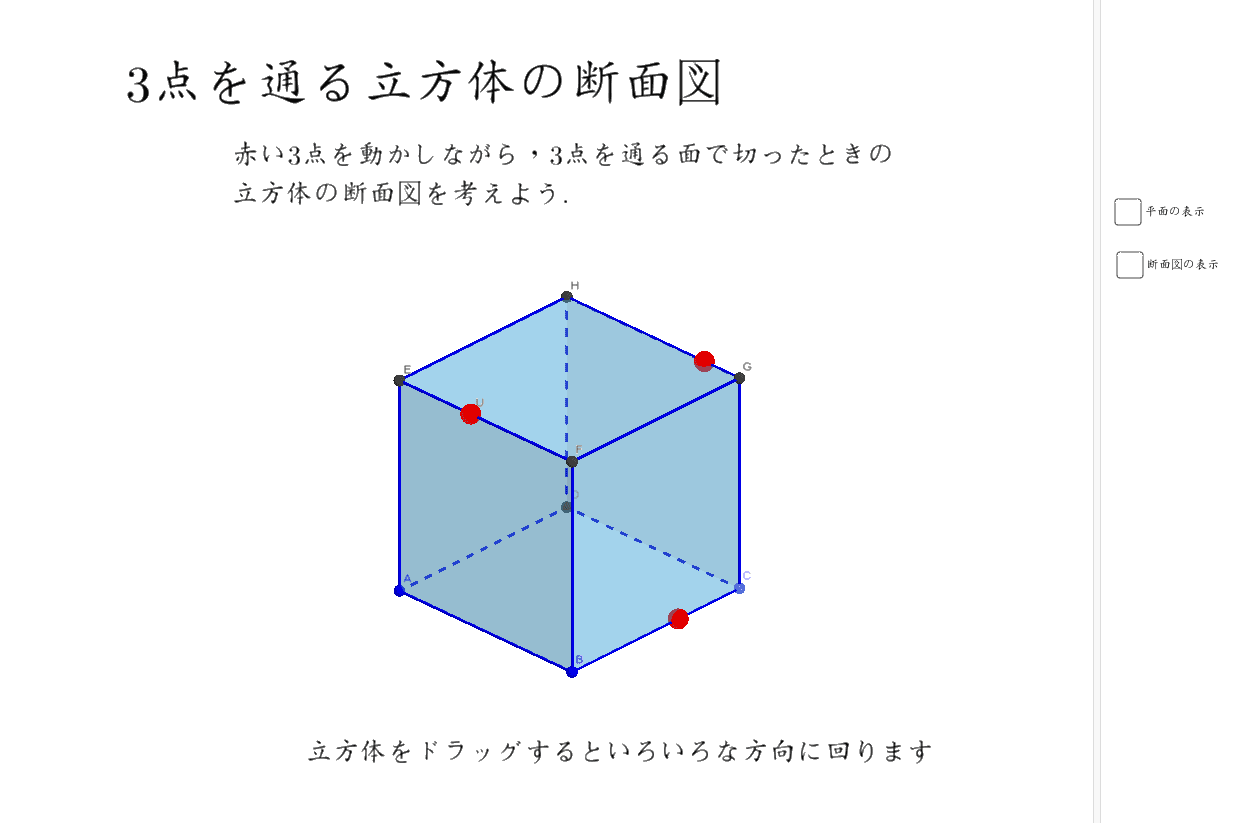



立方体の断面図 Geogebra



駒場東邦中より 複雑な立体切断を基本定理に落とし込みます 07 06 04 学習塾ロジム 今週の1問
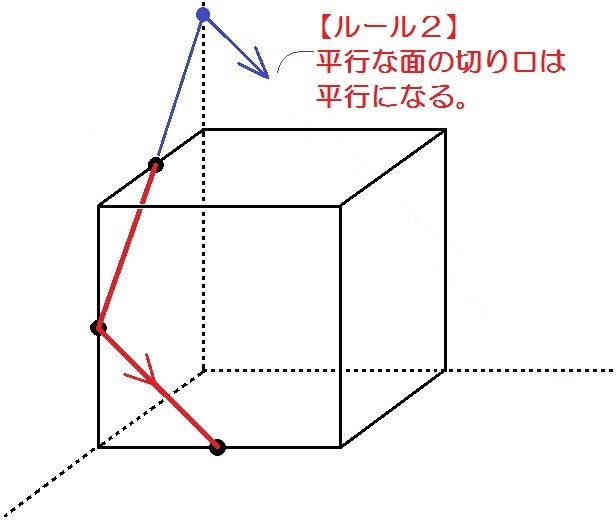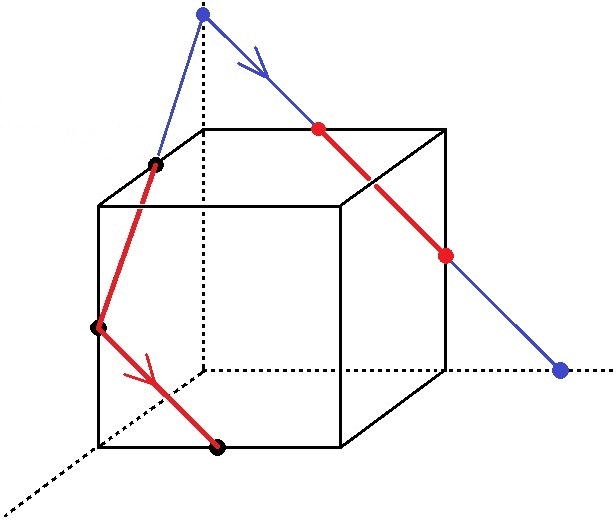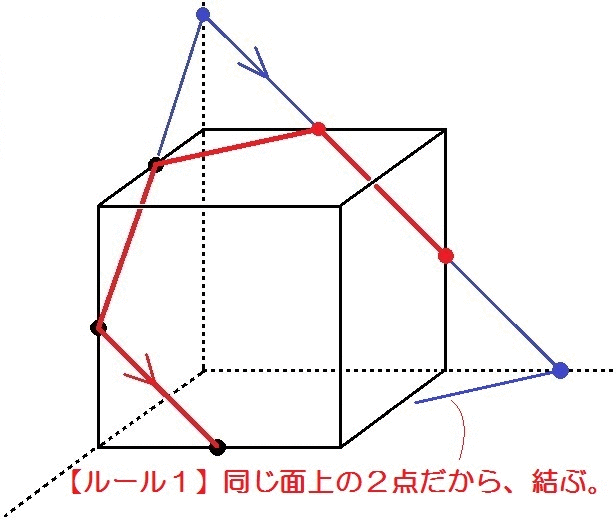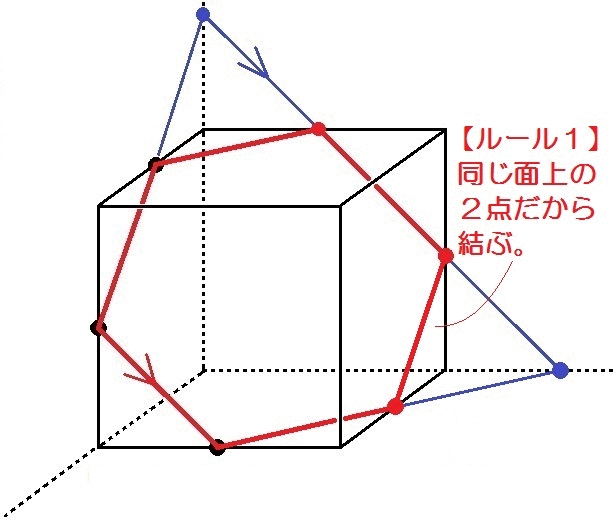



中学数学 空間図形 立体の切断問題のコツ




問題174 立方体に潜む正多角形



Math 空間図形 立体の切断と切り口 働きアリ The 2nd




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり




立体切断 その4 中学受験算数の家庭学習教材 カンガループリント



中学数学 立体の切断面 中学数学の無料オンライン学習サイトchu Su




直方体を切り取った図形の面積 数学i By Okボーイ マナペディア



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ



3



立方体の切断 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



2



攻玉社11 5 の 1 立体図形 立方体を平面で切断したときの体積と表面積 気まぐれ解説カフェ 仮



よく見かけますね この展開図 後編 中学受験プロ講師ブログ
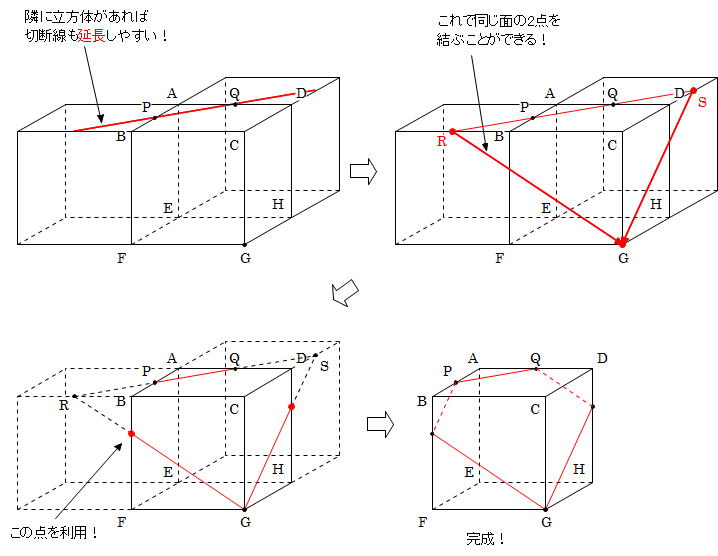



14年度 中学入試分析11 切断面の面積比 前田昌宏の中学受験が楽しくなる算数塾
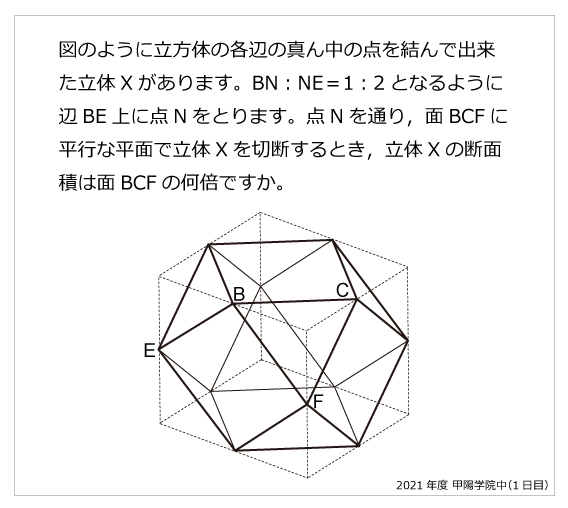



立体の切断 算数星人のweb問題集 中学受験算数の問題に挑戦



みんなの算数オンライン 中学受験 5年 立体図形3 立方体の切断1 例題と解説
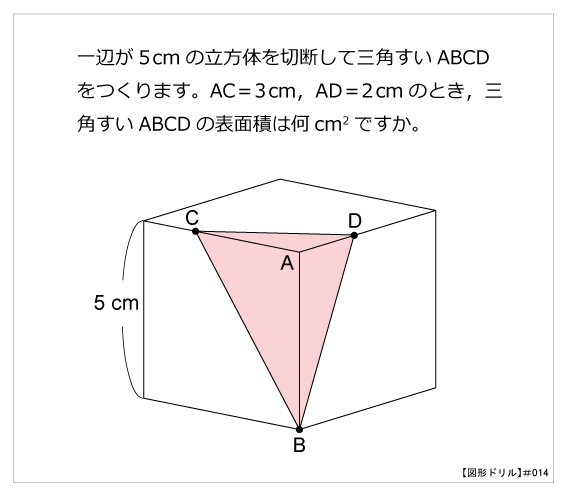



図形ドリル 第14問 三角すいの表面積 算数星人のweb問題集 中学受験算数の問題に挑戦



1




北辰塾 情報局 直撃 中学入試問題 第213回 本郷 体積 立方体の切断




五つの立方体切断 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
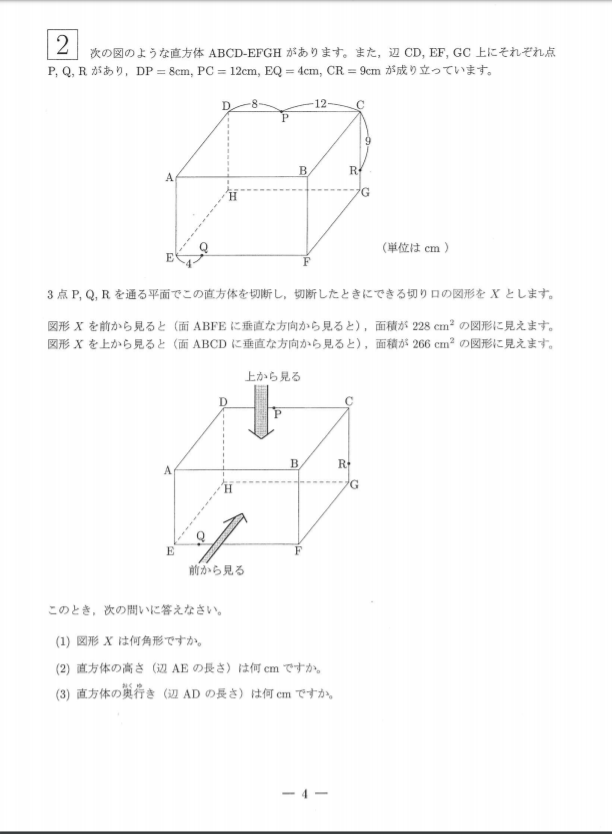



中学受験問題解説 必見 都内進学校生が難関中学の算数の問題を徹底解説してみた 開成中 編 東京受験 Jp




立方体の切断の問題 16年本郷中 元オカマの家庭教師の独り言



立体の切断 中学受験ブログ




イラスト入りでわかりやすい 立体切断の基本 無料プリントあり



第107問の解答



0 件のコメント:
コメントを投稿