壁から離れていく速さv' (はね返った後)が壁に近よ るる速速ささv (はね 返 る 前)の 何割 であるかの 比 がはね 返り係数 e である. v' e = v ※弾性衝突の場合,e = 1となる. 平均の速度と瞬間の速度の違い! 速度がわかるxtグラフ! 『 速度 』とは、「単位時間あたりの変位を表したもので、速度=変位÷かかった時間」でしたね。 そして、『 速さ 』とは、速度の大きさです。 今なら、こういう問題は、すぐに解けちゃい1物理では、速さの他に運動の( )まで含めた量を速度という。 2一定の速さで、一定の方向に進む運動を( )運動という。 3等速度運動をする物体は、一直線上を一定の速さで進むので、この運動を ( )運動と呼ぶこともある。

波の振幅と波長の求め方は分かったのですが速さvの求め方が分かりません Clear
速さを求める 物理
速さを求める 物理-瞬間の速度が、微分を用いて求まるのはなぜですか? 〔回答〕 「距離÷時間」の極限を考えているためです。 「距離÷時間=速さ」なので、この極限は瞬間的な速さということになり、数学的には「微分」の作業に相当しています 運動時間が10秒かつ速度を求めたい→①の公式を使う 求める初速度をv0とすると、 0=v0(2)×10 よってv0=(m/s) 止まっていた男性が一定の加速度で加速しながら進みだした。 6m進んだ時に秒速6mで進んでいた時、この人の加速度はいくらか
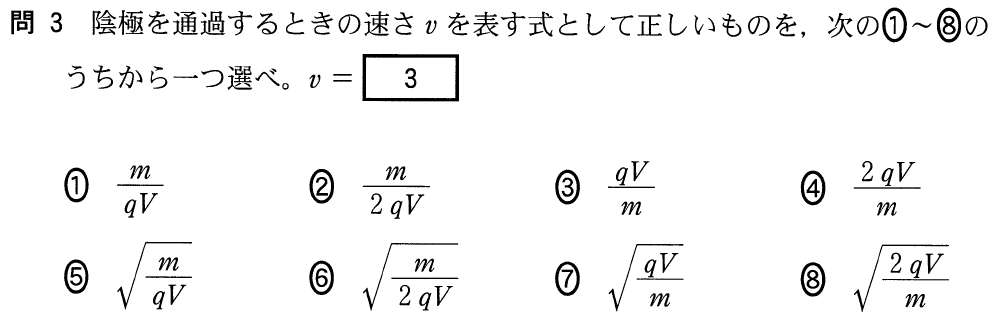



センター17物理追試第2問b 電場中 磁場中における荷電粒子の運動 理科が好き Com
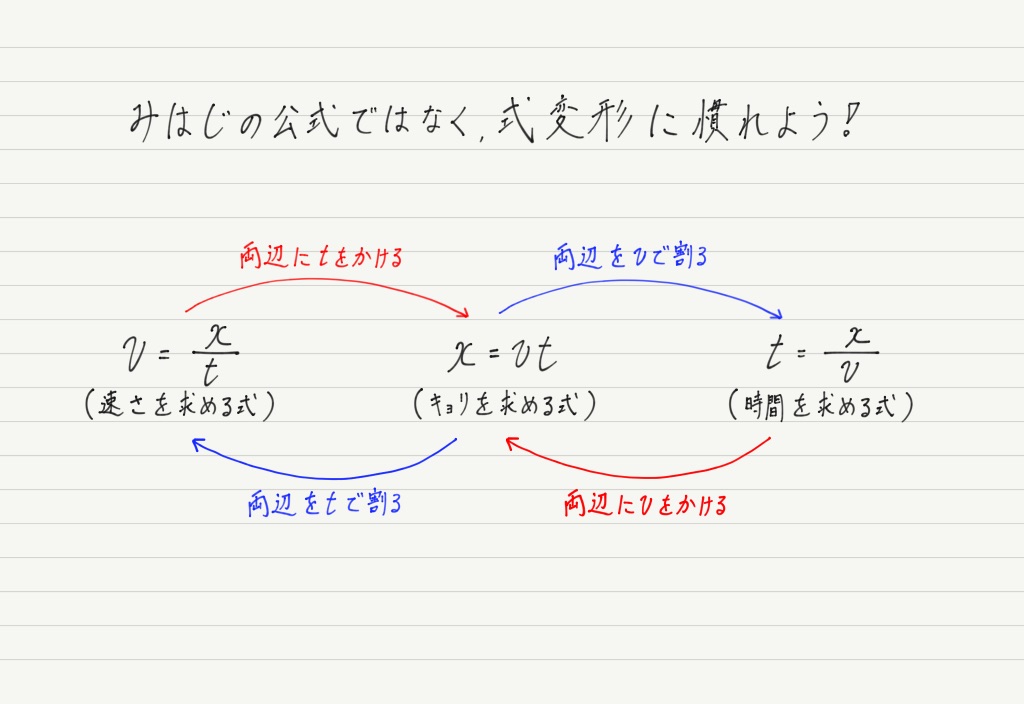
速さと速度の違いを知っておくことは基礎物理のはじめですね。 速さ、速度は良く聞くけどどう違うのかが説明され混乱するのではないでしょうか。 もちろん定義があって約束されているのですがあまり深く考えなくて良いです。 何故かと高校物理 ボルツマン定数と分子の平均速度の導 5分でわかる光の速さ!秒速や時速、地球何周? 1849年には、フランスの物理学者アルマン・フィゾーが、歯車と鏡を使って光の速さを求めました。速さを求めたいときには、 速さ=距離 ÷ 時間 という公式を使います。 例えば、距離 30 k m の道のりを、 3 時間かけて進んだときの速さは、 距離 ÷ 時間 = 30 ÷ 3 = 10 つまり、 時速 10 k m です。 公式を忘れても、はじきの図で求めたいものを隠すことで
距離を時間で割れば波が伝わる速さが求まるので、求める波の速さv は、波長λ を時間T で割ることで求められます(右図)。速度の求め方と変化量を表すΔ(デルタ)>高校物理 If playback doesn't begin shortly, try restarting your device 物理基礎力学03<速さと速度の違い物理基礎力学補講『速度と加速度 〜平均と瞬間〜』の講義内容に関連する演習問題です。 講義編を未読の方は問題を解く前にご一読ください。 速度と加速度 〜平均と瞬間〜 小学校の算数を思い出しましょう! 「10分で800m歩いた人の速さは分速何mですか。 」計算は簡単。 速さ = 800m ÷ 10分 = 80m/分です。 この人は10分間ずっと同じ速さだったのでしょう
例題:下図のように、速さ m/sで動くAが、速さ10 m/sで動くBに衝突した。衝突後、Aの進む向きが逆になり、速さは50 m/sになった。このときの反発係数を050とすると、衝突後のBの速さを求めよ。速さ=波が1 sに進む距離 さらに手を上下に何度も振動させると、波はどんどん右に進んでいきます。 このとき、波が1 sあたりに進む距離が 速さ となります。 速さ は v m/s と表します。 波の速さvはどう計算できるかわかりますか。 波が1回振動するのに要する時間が 周期T s で、1回の振動によって進む波の距離が波長λ mでした。 速さは、1 sあたりに進んであり、t 秒後の紙面こちら向きの速さは * v = v 0 at 閉じる \(\large{\frac{qE_1}{m}}\)t であり、 この速さを v 0 と合成しますと(三平方の定理より)、 \(\sqrt{{v_0}^2\big(\frac{qE_1}{m}t\big)^2}\) (




波の振幅と波長の求め方は分かったのですが速さvの求め方が分かりません Clear




速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に
「平均の速さ」は、「全体の移動距離(変位)」÷「その移動にかかった時間合計」。合計の時間でいくら進んだのか、の事です。 「瞬間の速さ」は、ある秒数間でいくら進んだか、の事です。例えば、2秒目〜3秒目間で、5m進んだなら、その時の瞬間の速度は、5 m ÷(3落下運動 物理基礎+物理 落下運動 重力加速度 空気抵抗が無視できれば,物体はその質量に関係なく,同じ加速度で落下 する * 。地上付近で,物体が重力のみを受けて落下するときの加速度を重力加速 最速降下曲線を求める 前置きが大変長くなりましたが,計算に入ります. 変分法1 の基礎が分かっていることが前提になっています.またベルトラミの公式を使いますので忘れてしまった人は先に 変分法2 を復習して下さい. 最終的に求めたいのは関数形 ですが,変分法の問題ではま
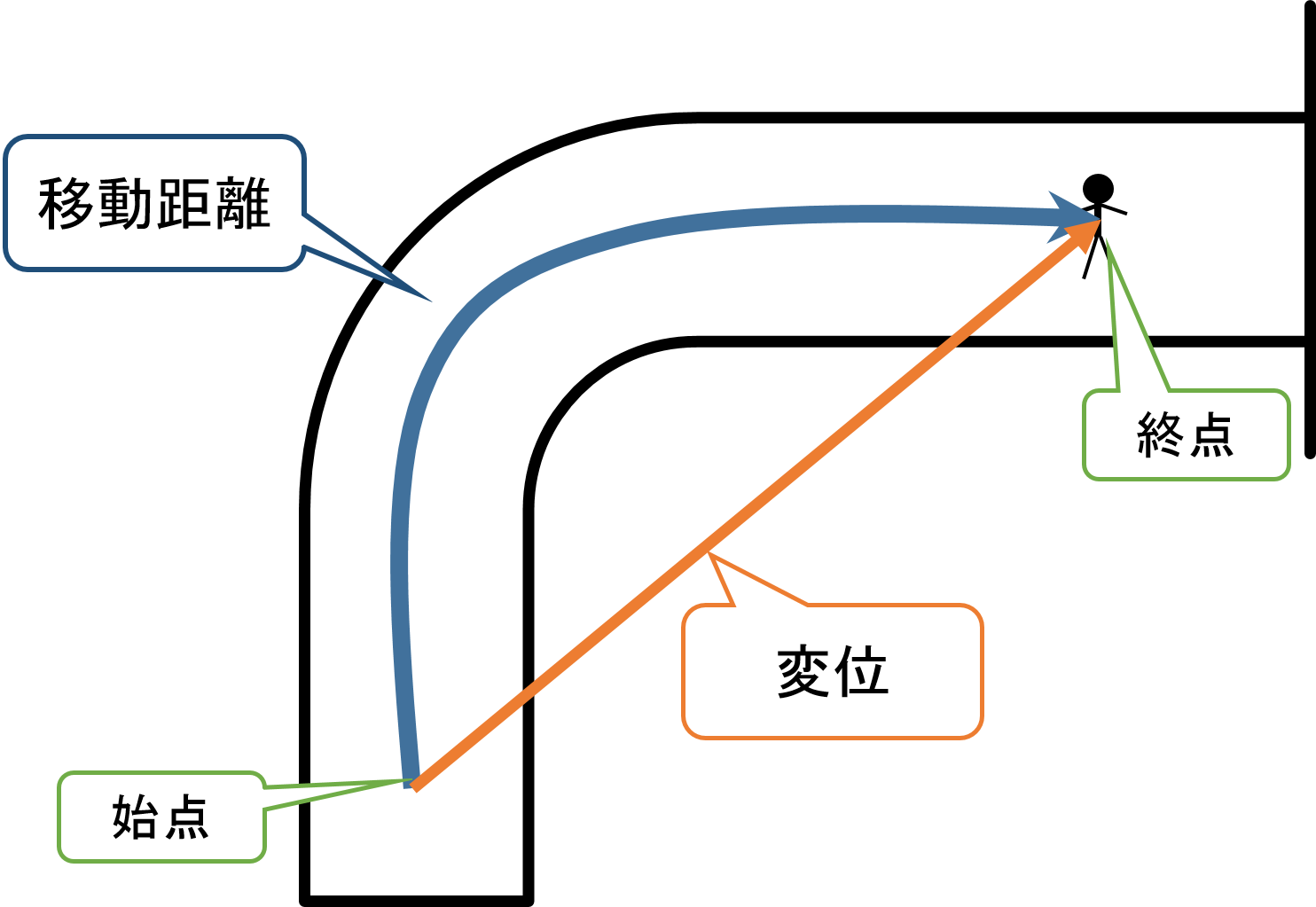



移動距離と変位 速さと速度の違いを理解しよう 何を答えるかハッキリさせることが大切 平川ブログ
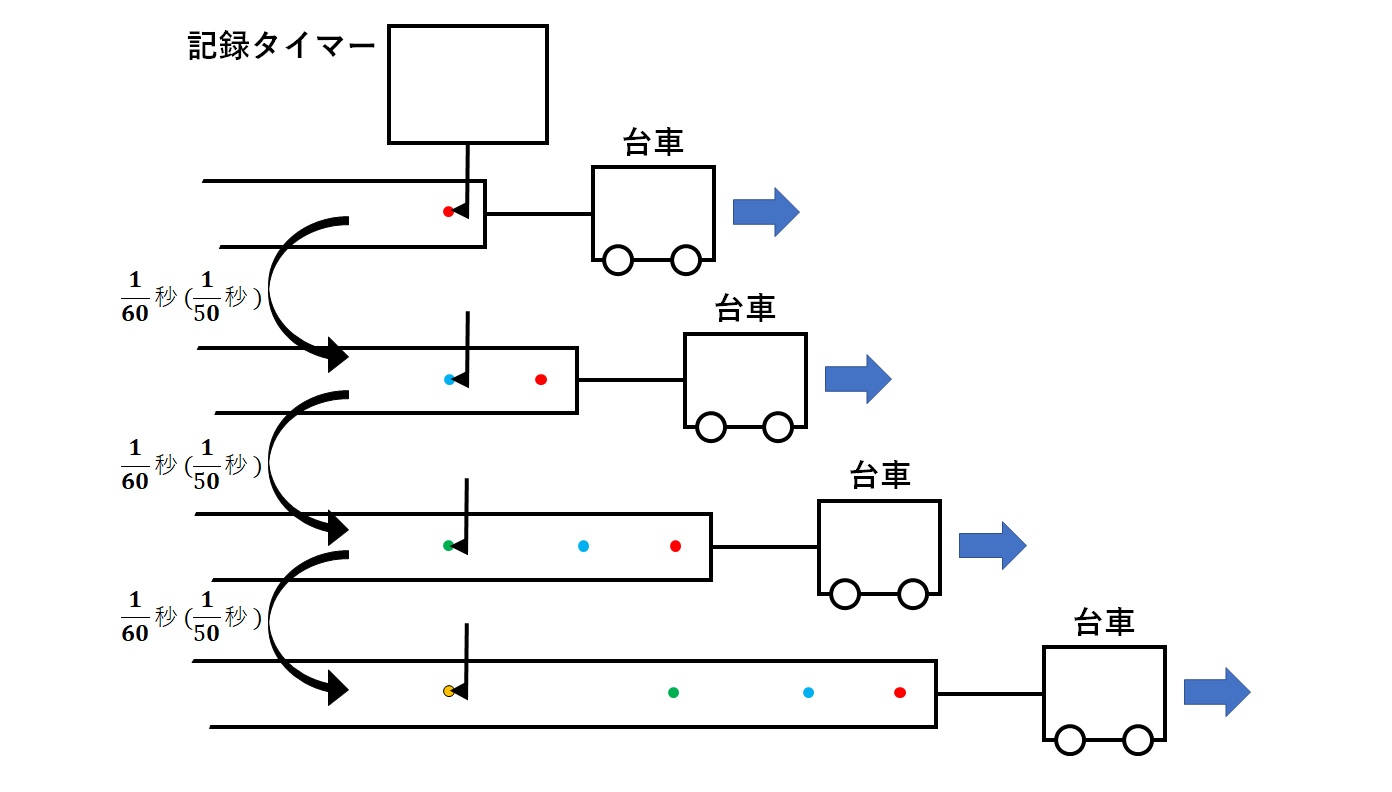



中3物理 速さ 記録タイマー 中学理科 ポイントまとめと整理
X方向の分子の速さはv x なので、t=2L/v x ですね。 分子が壁に1回あたるのに必要な時間はts/回となります。 したがって、1sあたりの衝突回数は求めたtの 逆数 で求められます。 色々な変形オイラー方程式 1 f=f (x,y') 2 f=f (y,y') 3 f=f (x,y) 4 f=f (x,y,y',z,z') 5 f=f (x,y,y',y'') 6 f=f (x,y,y',,y^ { (n)}) 7 f=f (x_ {1},x_ {2},u (x_ {1},x_ {2}),u_ {x_ {1}} (x_ {1},x_ {2},x_ {3})),u_ {x_ {2}} (x_ {1},x_ {2},x_ {3})) 例題(運動方向の加速度を求める) 小物体の質量を m としますと、小物体には mg の重力がはたらいています。 その運動方向の成分は mgsinθ です。 小物体の加速度を a として運動方程式を立てますと、 ma = mgsinθ となり、計算しますと、a = gsinθ です。 これはつまり重力が sinθ 倍に小さくなったと
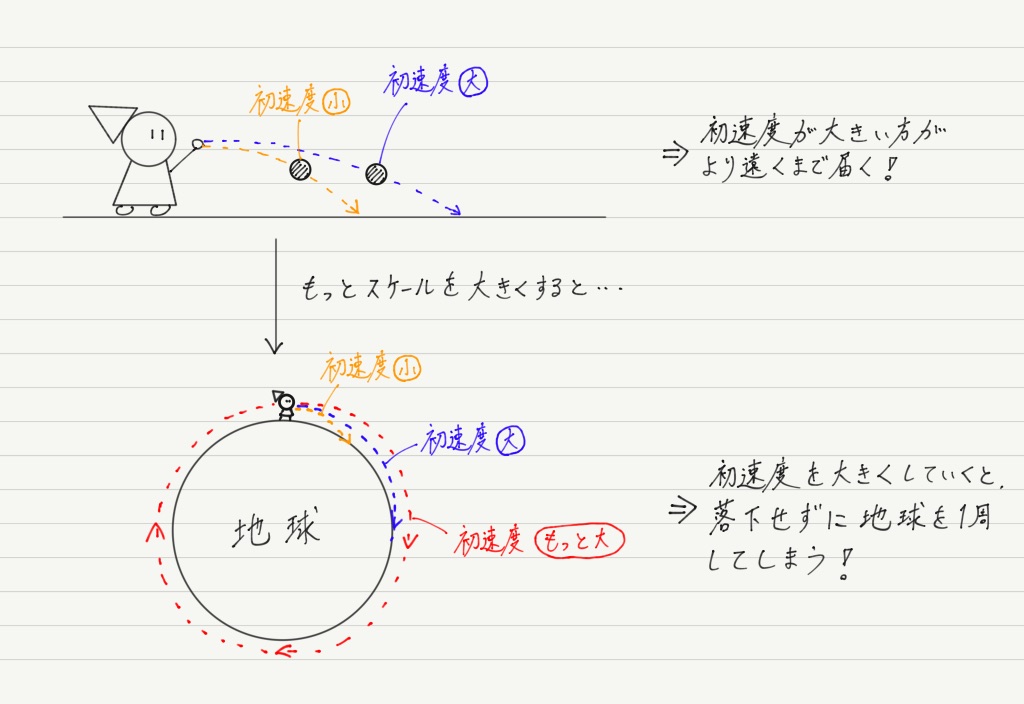



万有引力を受ける物体の運動 高校物理をあきらめる前に 高校物理をあきらめる前に



平均の速さと瞬間の速さ 3年理科 物理 Takaの授業記録04
よって、t1=0s ,v1=0 m/s ,t2=30s ,v2=30 m/s として(1)式に値を代入して平均 加速度を求めると、 a= v2−v1 t2−t1 = 30−0 30−0 = 30 30 = 10 m/s2 (2) よって、時刻t= 10sの時の加速度は、10 m/s2 と求まった。 これは時刻t= 0から時刻 t= 30sまでの平均加速度であり、この間一定である。 (2)前の問題と同様に、時刻t= 100sから、t= 150sまでは加速度は変化していないので、時 刻t= 平均の速さの求め方 平均の速さを求めるときに、平均だからといいすべての「速さ」を足して、その数で割るという意味ではありません。 (例えば、10 m/sで100 m移動し、その後 m/sで100 m移動したとき、平均の速さは15 m/sになりません。の速さは、 となる。 1秒間の波の数= 振動数f vf 時間t 距離x 波源 振幅A、波長 、周期Tの正弦波 の任意の時刻t、任意の距離x に おける波D は、 で表される。ただし、 0は初期位 相。 0 (,) sin2 tx Dxt A T 波の進む速さ



微分を使って瞬間の速さを求めよう 木倍川物理部 キマシスタ




平均の速度と瞬間の速度の違いとは 公式および求め方
周期(時間)は\ {(距離)}{(速さ)}={2π r}{v}\ で求められる\ 半径はRhであることに注意 後は静止衛星の周期と自転周期をイコールにした後,\ hについて解けばよい 高校物理I 『速さ / 求め方 / 単位の変換』 高校 物理 速さ 速さの求め方 単位 単位の変換 physics このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます!微分を使って瞬間の速さを求めよう 今回は微分を使って瞬間の速さを求めてみましょう! 前回の記事 ではこんなグラフが登場しました。 一定の加速度で加速している場合の距離と時間の関係です。 赤のグラフがx=2t 2 青のグラフがx= (1/2) t 2 グラフ上の
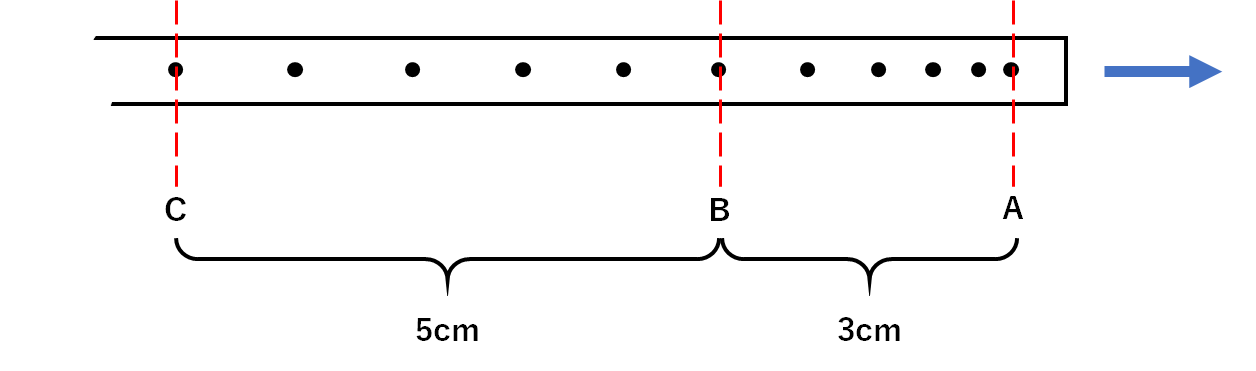



中3物理 瞬間の速さ 中学理科 ポイントまとめと整理
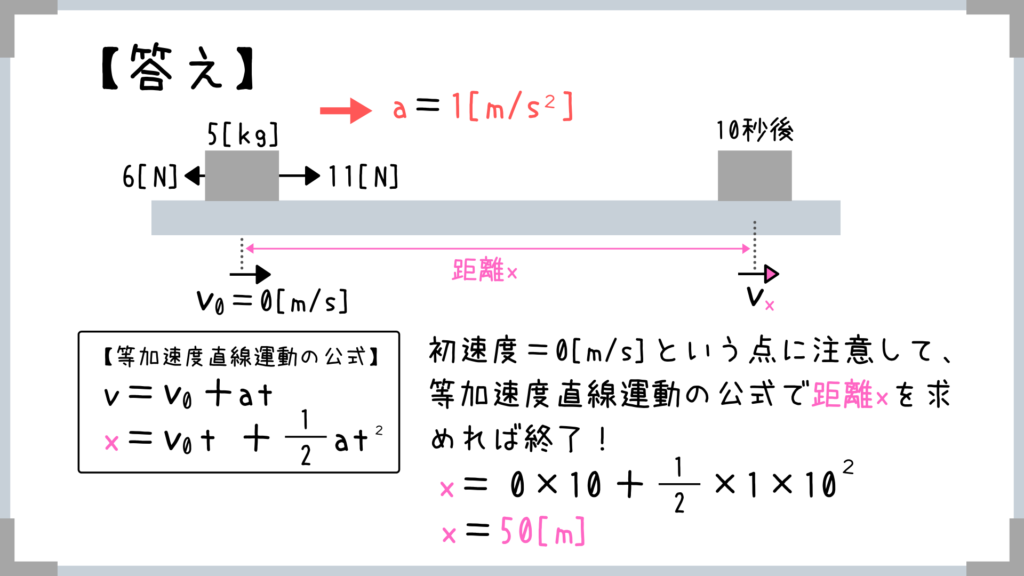



力学 物体の運動 賢い人は公式を覚えない 物理の考え方をマスターしよう せんせいの独学公務員塾
(162) (161) で求めた力の大きさは 何kgw か。 1 kgw 98 N 600 kgw 98 kgw 5,0 N 5,0 (163) ブレーキをかけ始めてから何秒後に 停止したか。 t 秒後の速さ v(t) 18 6 t m/s t0 秒後に停止 v(t0 ) 18 6 t0 0 3秒後 従って、 3 s 6 m/s 18 m/s 0 2 t



平均速さと瞬間の速さ物理 2 教えてください Yahoo 知恵袋




高1の物理基礎です Clear




瞬間の速さと平均の速さ 塾の質問箱




中3理科 平均の速さと瞬間の速さ 練習編2 映像授業のtry It トライイット
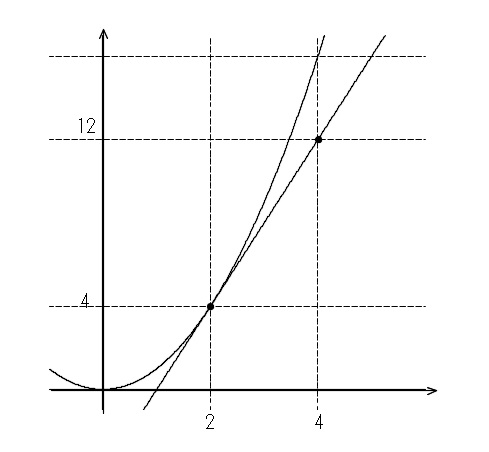



平均の速度と瞬間の速度の違いとは 公式および求め方




高等学校物理 物理i 運動とエネルギー 物体の運動 Wikibooks
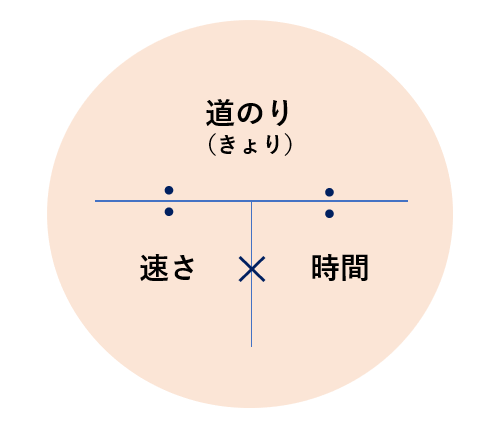



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは
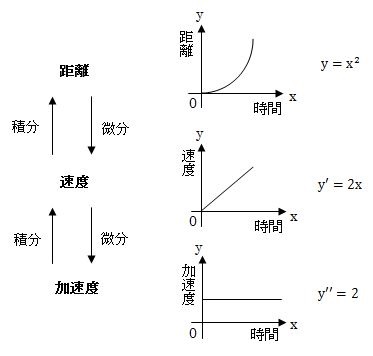



加速度 速度 距離の関係 もう一度やり直しの算数 数学



高校物理難問です車輪の外周の速さと中心の速度の関係が見出せません車輪 Yahoo 知恵袋
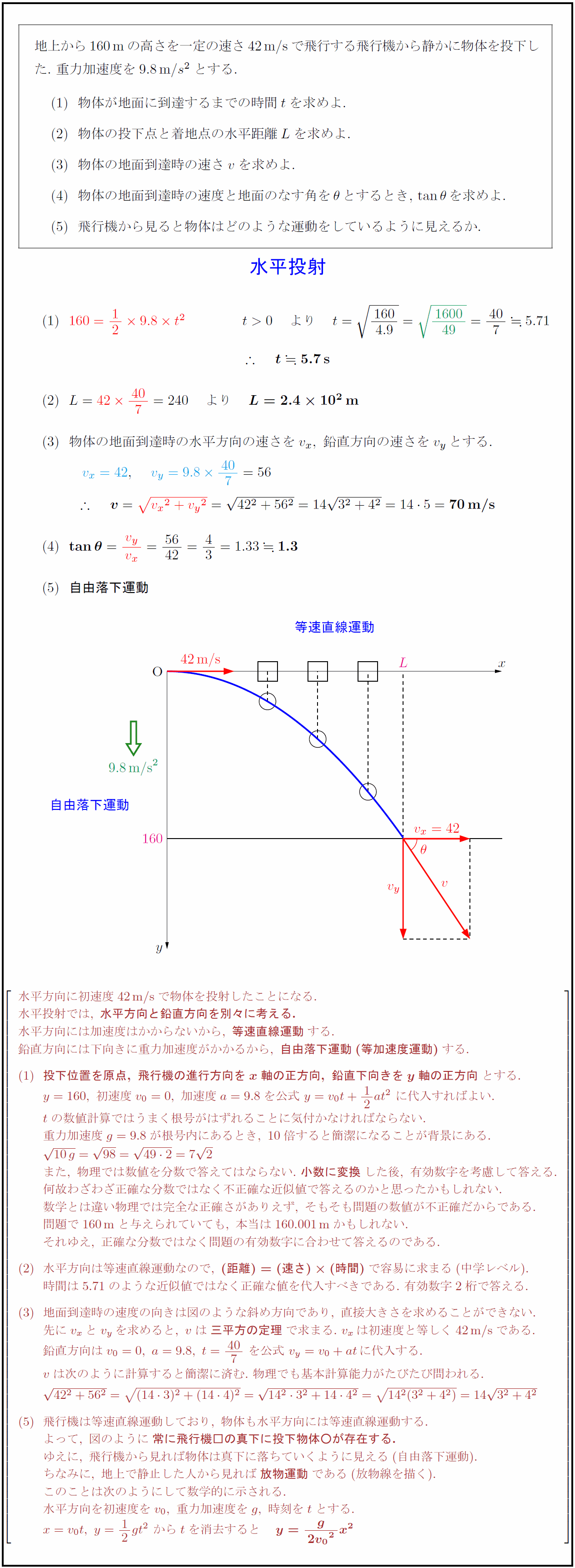



高校物理 水平投射 受験の月




高校物理 速さ Youtube




しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは




センター17物理追試第2問b 電場中 磁場中における荷電粒子の運動 理科が好き Com



単振動



平均の速さと瞬間の速さ 3年理科 物理 Takaの授業記録04
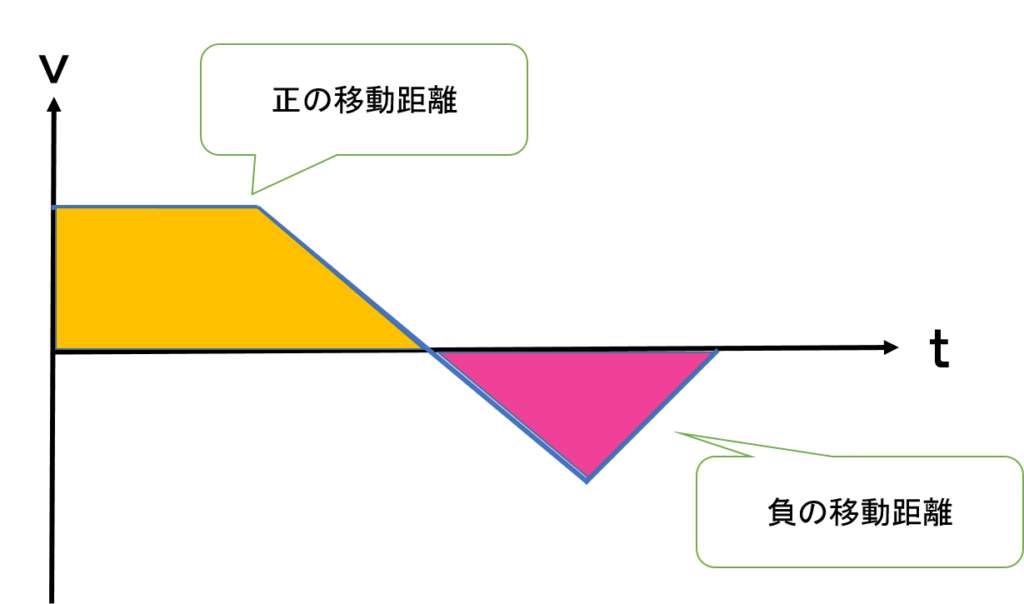



x tグラフとv tグラフ 傾き 面積などの書いてあるグラフの注意点を学ぼう 平川ブログ




速さと運動 Ict教材eboard イーボード
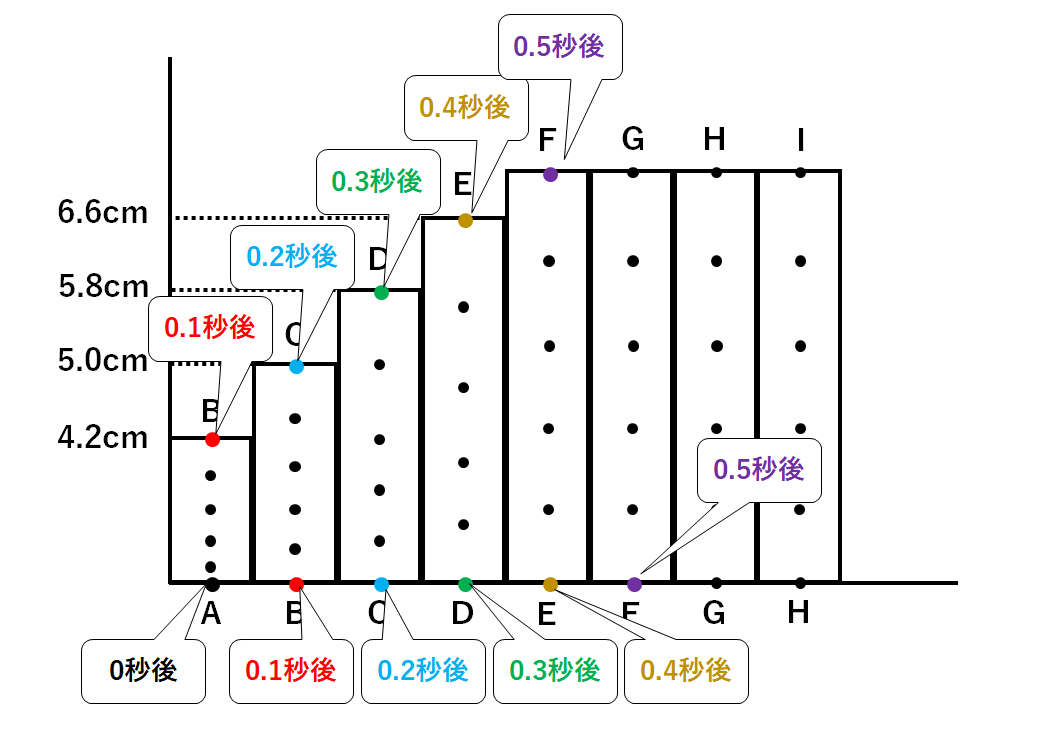



中3物理 速さ 記録タイマー 中学理科 ポイントまとめと整理




なぜ 変位は 面積 変位なのですか Clear



物理の基本 運動を 速度 で表現する 文系にこそ読んでほしい高校物理のコツ文系にこそ読んでほしい高校物理のコツ




中3理科 平均の速さと瞬間の速さ 練習編2 映像授業のtry It トライイット



3




等加速度直線運動の3公式の使い方がわかりません 理科 苦手解決q A 進研ゼミ高校講座




物理 瞬間の速度 Youtube




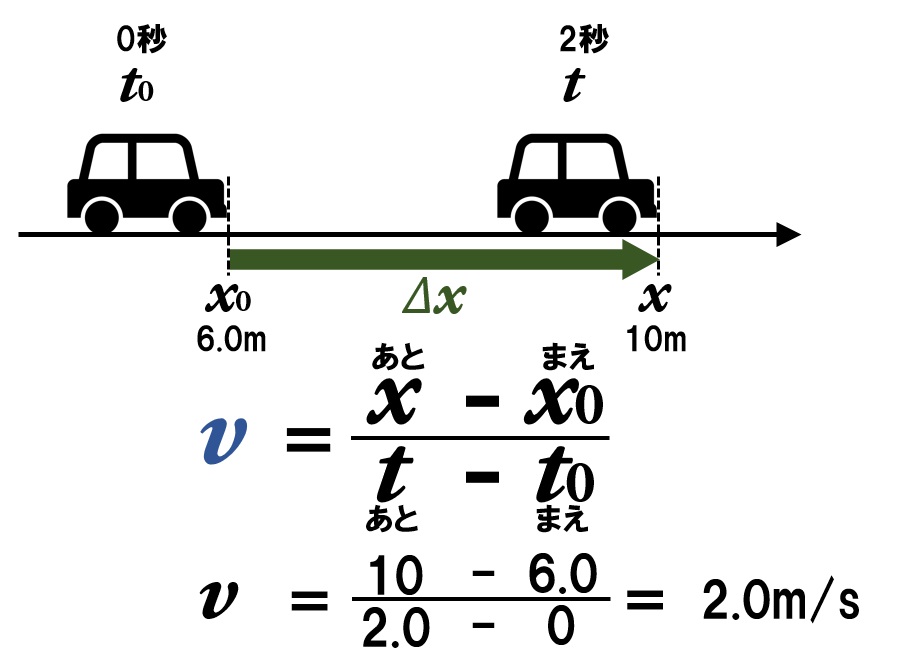
平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




高校物理 速度の合成と分解 Youtube




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




高校物理 物理の初めの一歩 速さ 力学 お茶処やまと屋
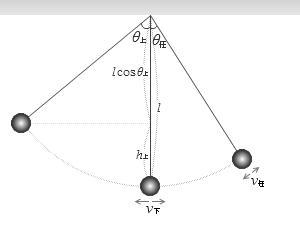



単振り子の力学的エネルギー わかりやすい高校物理の部屋



等速直線運動 高校物理をあきらめる前に 高校物理をあきらめる前に




高校物理 難関大入試によく出る 重心速度 力学 お茶処やまと屋



物理基礎の瞬間の速度についてどなたか教えてください 時刻 Yahoo 知恵袋
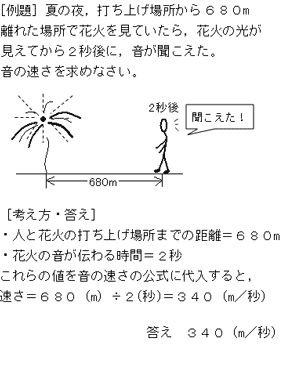



光 音 力 圧力 音の速さの求め方がわからない 中学生からの勉強質問 理科 進研ゼミ中学講座
.jpg)



光の速さはどうやってはかったのですか コカネット




物理基礎の 平均の速度の求め方がわからず困っています この問3の解 高校 教えて Goo




物理 物体の運動 問題演習 解説 高校生 物理のノート Clear




物理 平均の速さ 瞬間の速さ 厚木東 Youtube



1



あらい斜面をすべり下りる物体の運動 わかりやすい高校物理の部屋




高校物理 速さと速度 練習編 映像授業のtry It トライイット
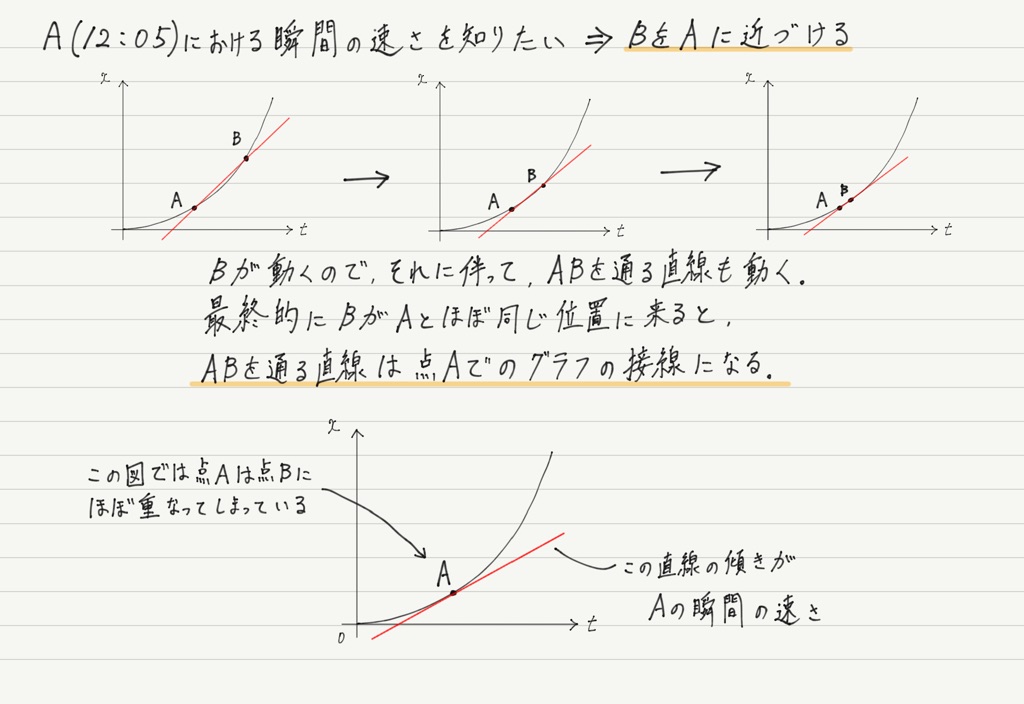



速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に



物理基礎 変位 速度 加速度 運動の基本情報 Tekibo




等加速度運動とは 3つの公式 グラフを例題とともにわかりやすく解説します 高校生向け受験応援メディア 受験のミカタ




中3 物理 速さの求め方 中学生 理科のノート Clear




平均の速さと瞬間の速さです が解説を読んでもわかりません Clear
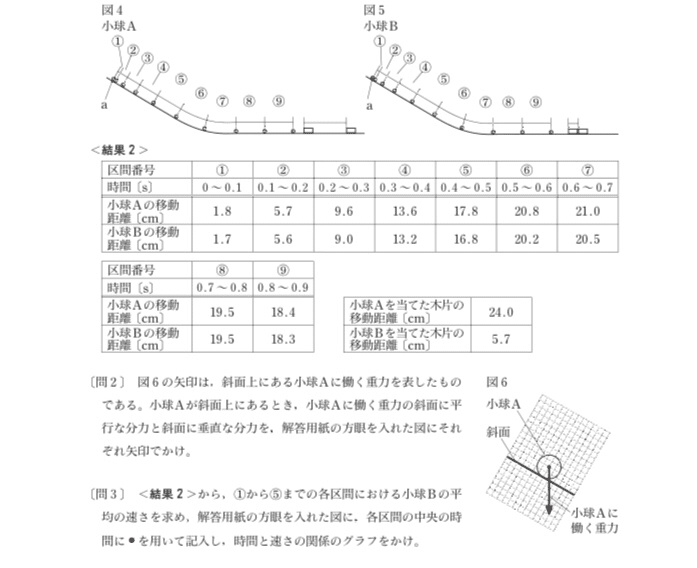



都立高校入試理科物理 平均の速さ 対策 坂本良太 Note
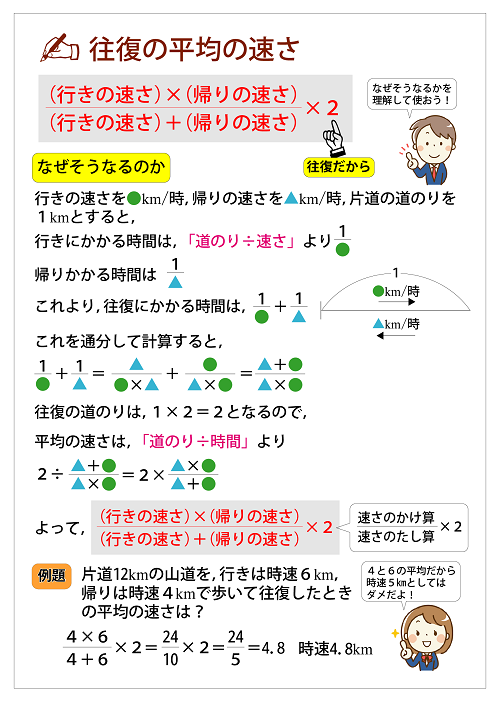



往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略



物理教室




X Tグラフとv Tグラフ 平均の速さと平均の速度 瞬間の速度とは ぷち教養主義




加速度とは 直線運動をする物体の加速度 速度の求め方 高校生向け受験応援メディア 受験のミカタ
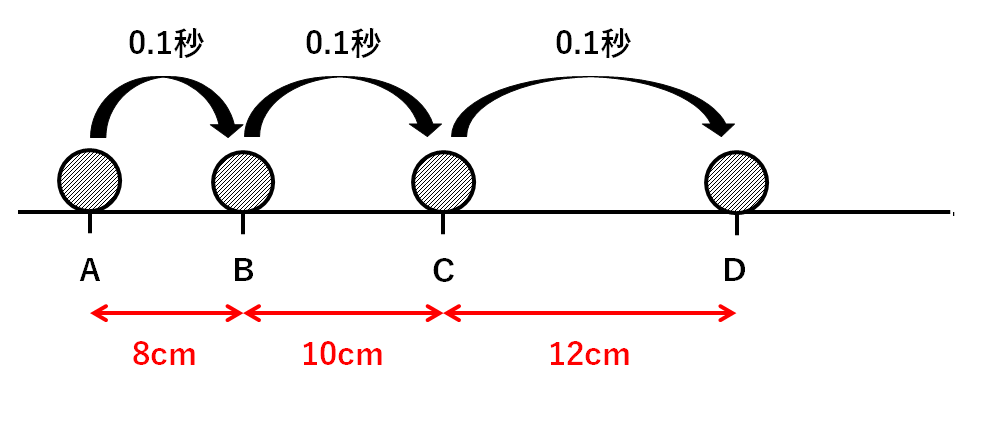



中3物理 速さ ストロボ写真 中学理科 ポイントまとめと整理




平均の速度と瞬間の速度の違いとは 公式および求め方




高校物理 難問でこそ使おう 相対速度 力学 お茶処やまと屋
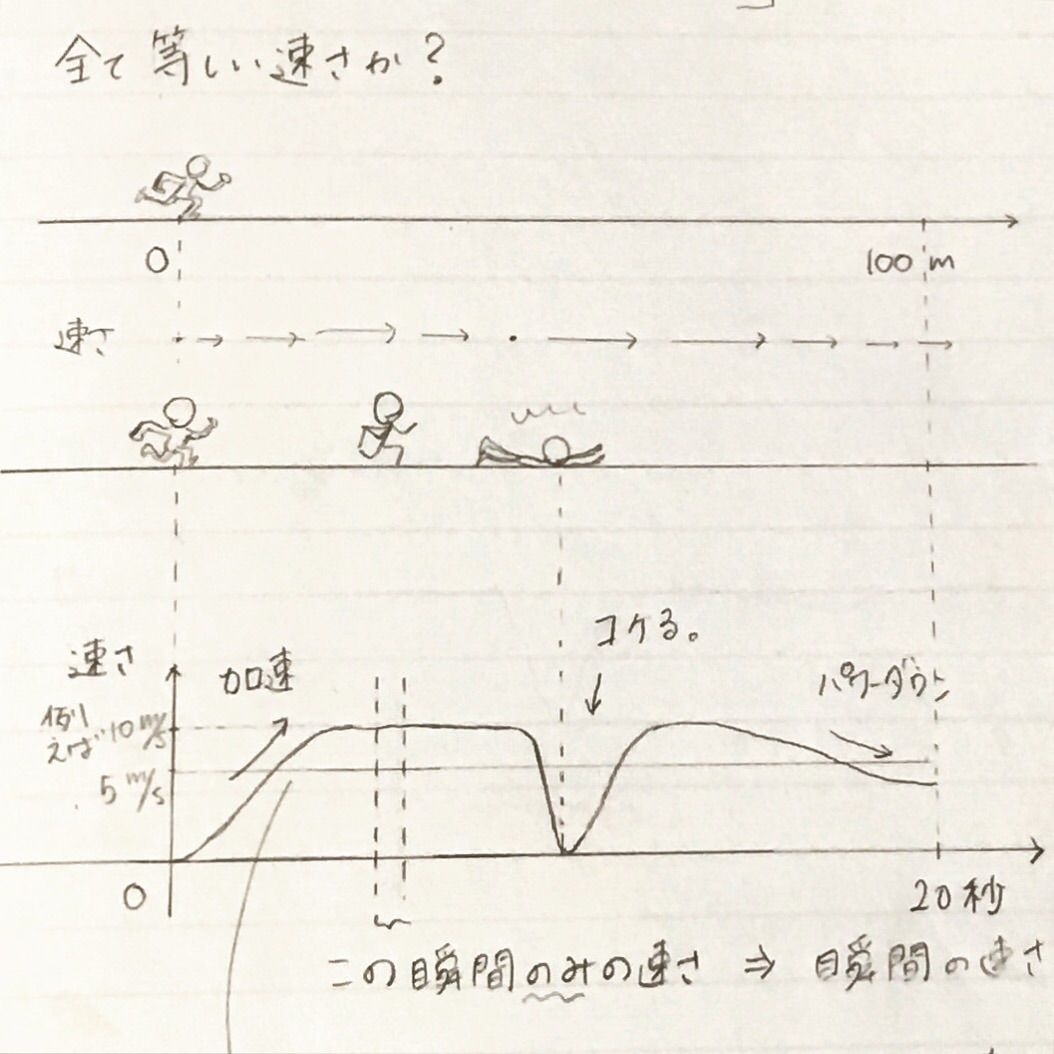



平均の速さと瞬間の速さ 高校物理をやさしく解説するブログ
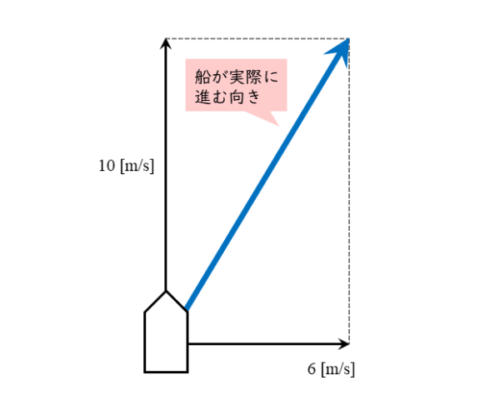



物理のヒント集 ヒントその4 流水を進む船の速度 日々是鍛錬 ひびこれたんれん
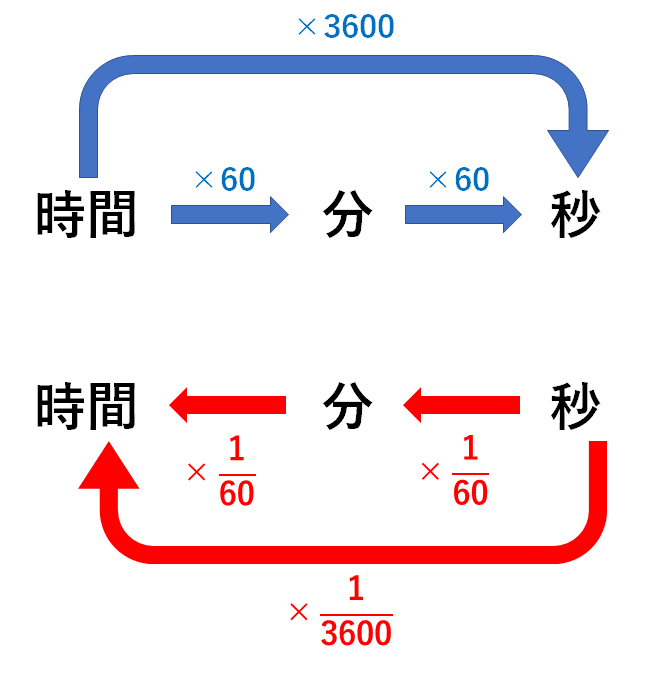



中3物理 速さの単位変換 中学理科 ポイントまとめと整理




しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室



物理の問題です 1 で 衝突直後の速さを求める時に 0の二 Yahoo 知恵袋




物理基礎 運動エネルギーの公式の求め方 物理 By 藤山不二雄 マナペディア




高校物理 一直線上の相対速度と平面上の相対速度 受験の月




V V0 Atの証明 導出 方法や微分 積分をしたらどうなるか 加速度と速さの関係 V V0 At 2は間違い ウルトラフリーダム




中3理科 平均の速さと瞬間の速さ 練習編1 映像授業のtry It トライイット




等速直線運動 高校物理をあきらめる前に 高校物理をあきらめる前に




高校物理 波長 L m 振幅 a m 速さ v m s 映像授業のtry It トライイット



Adoko 力学 物理基礎の力学21




速度と加速度の公式まとめ 微分積分も説明 理系ラボ




速度と加速度の公式まとめ 微分積分も説明 理系ラボ




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




物理基礎 運動と力01 速さと速度 16分 Youtube
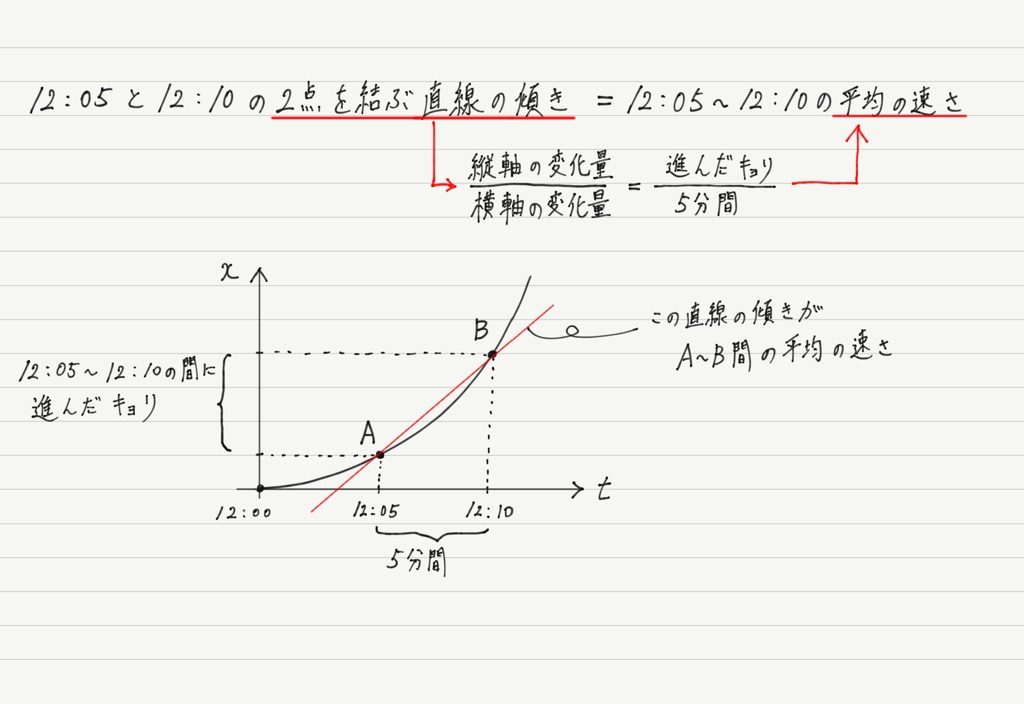



速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に




高校物理 仕事wと仕事率p F Xグラフ 仕事率pと速さvの関係 受験の月




高校物理iの 瞬間の速度 と 速度 についてです 画像の 瞬間の 教えて Goo
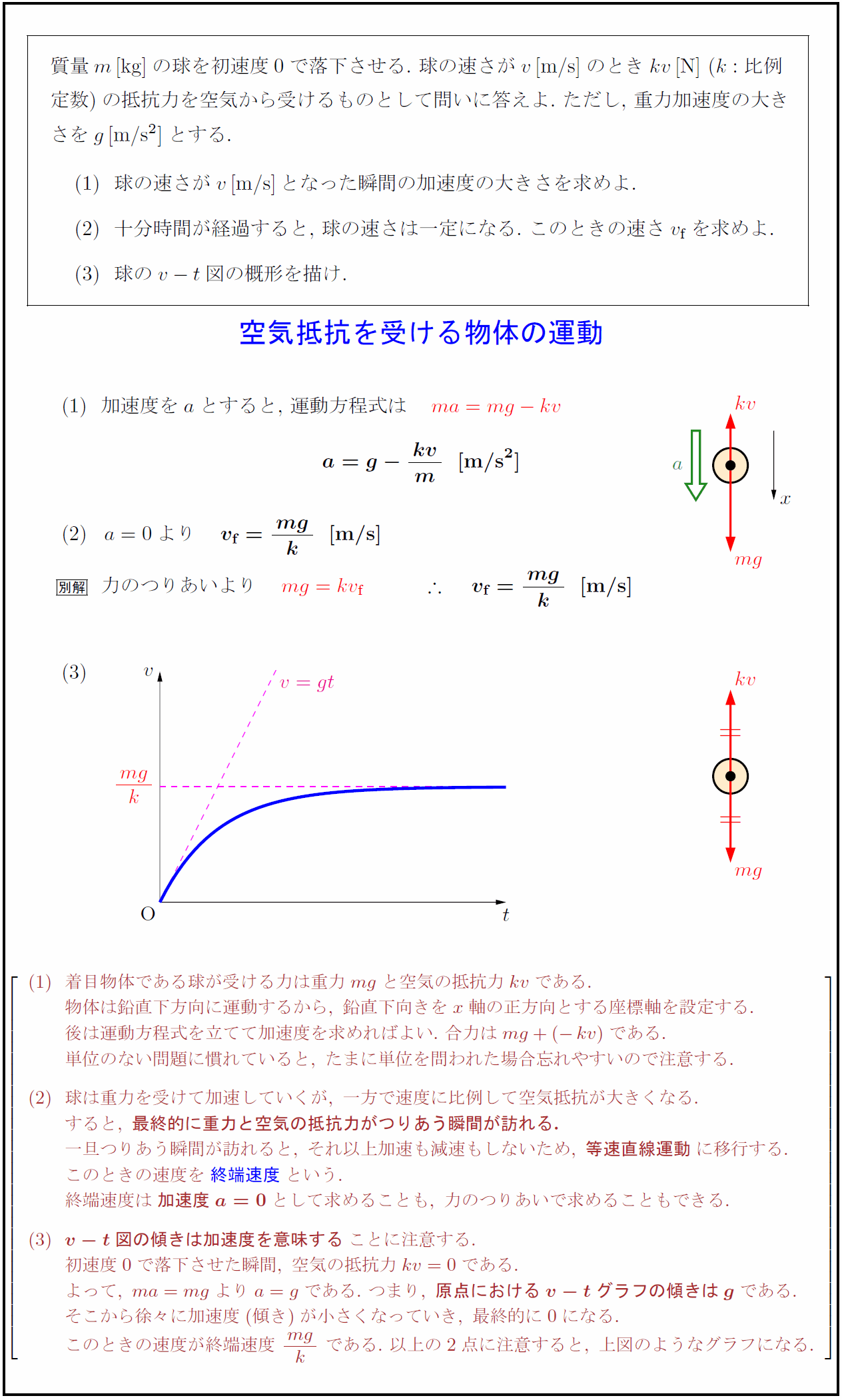



高校物理 空気抵抗を受ける物体の運動とv Tグラフ 終端速度 受験の月



Adoko 力学 物理基礎の力学21




高校物理6 5 平均の速さ 講義 物理基礎6 5 Youtube
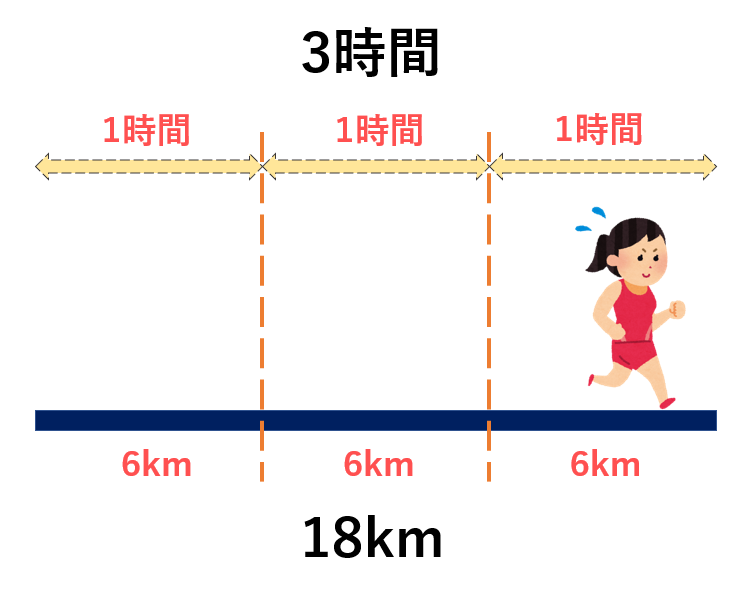



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社



高校物理です この写真の問題の の衝突直後の速さを求める場合になぜx方向に注目 Yahoo 知恵袋



1




速度と加速度の公式まとめ 微分積分も説明 理系ラボ




運動エネルギーの公式とすぐにわかる求め方 運動エネルギーの変化とは 高校生向け受験応援メディア 受験のミカタ
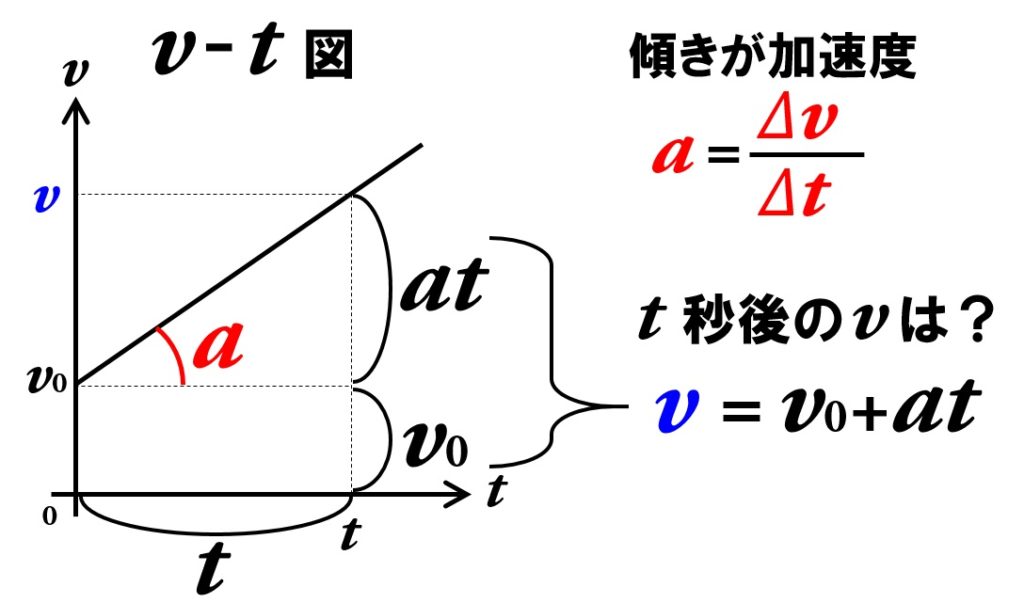



物理基礎 等加速度直線 公式の導出と練習問題 Tekibo
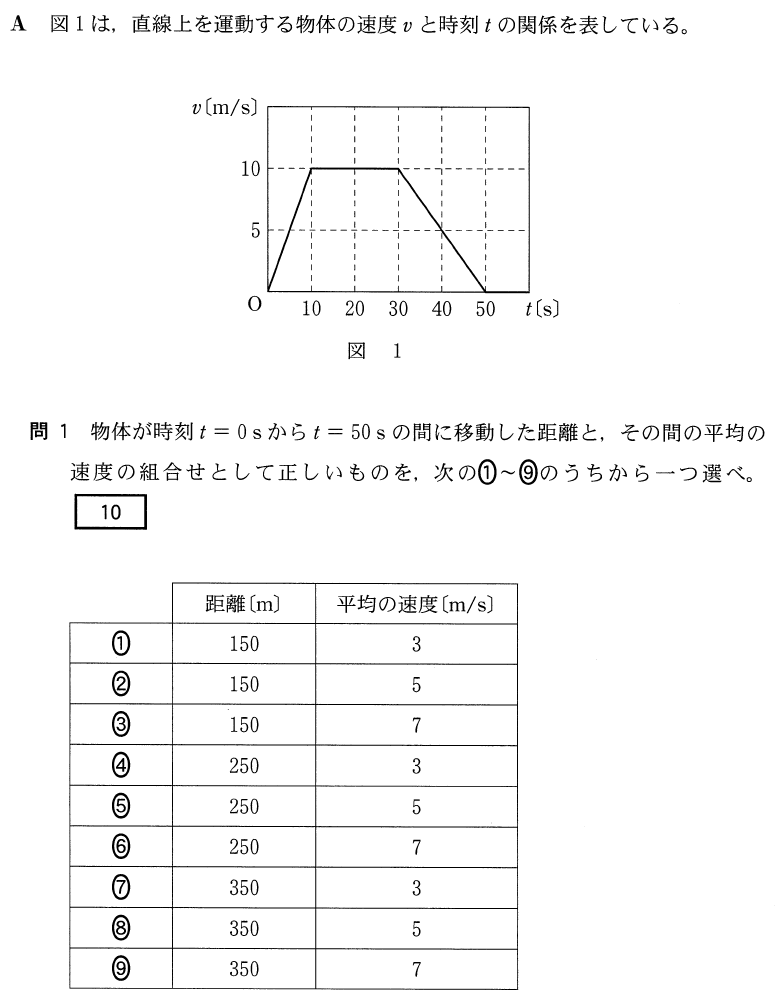



センター 15物理基礎追試第3問a V Tグラフとa Tグラフ 理科が好き Com



音の速さの計算問題をくわしく解説




中3理科 速さの計算 映像授業のtry It トライイット



Uor642eo9ah87f Com E7 B5 E7 Ab Af E9 80 9f E5 Ba A6 81 A3 81 A6 E4 95 Ef 9f E7 Ba E6 B0 97 E6 8a B5 E6 8a 97 81 8c 81 8b E7 E4 93 81 Ae E9 81 8b E5 8b 95 81 Ab 81




物理 瞬間の速さ 平均の加速度 Youtube




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




速度と速さの違いって 速度を定義しよう 物理のいろは
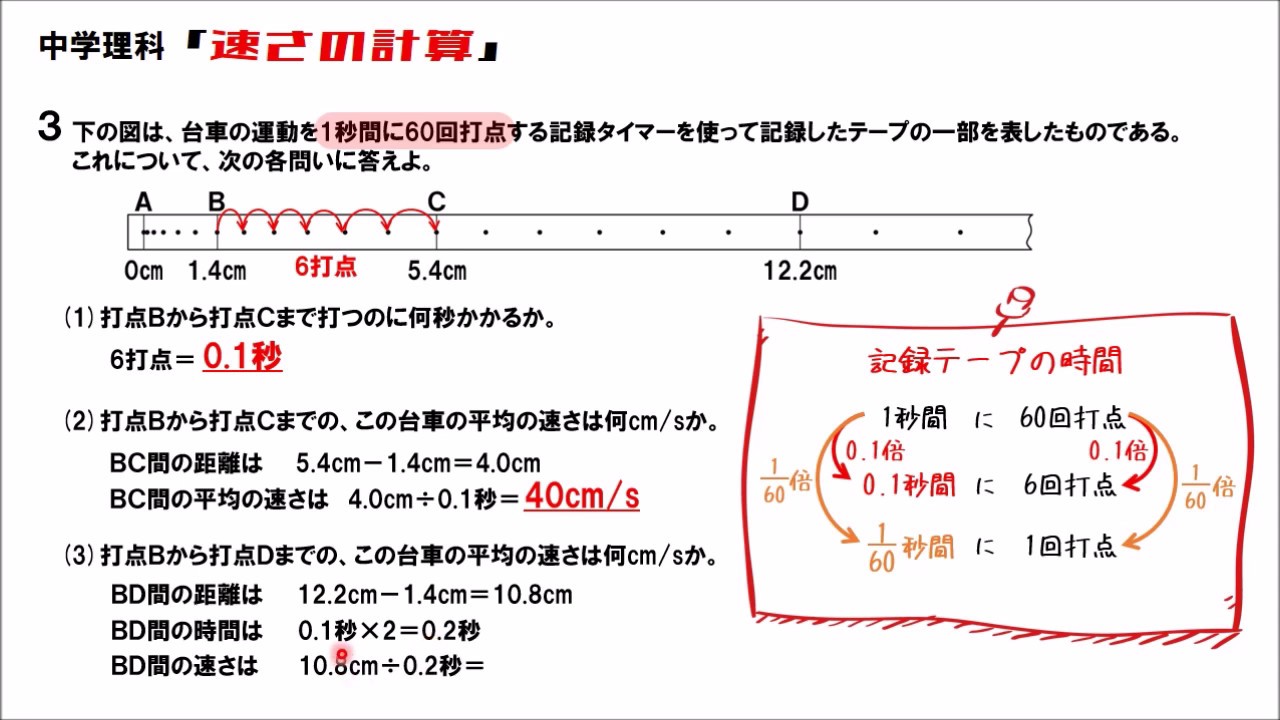



中学理科 速さの計算 Youtube



3




速さと速度の違いとは 公式を具体例で確認



0 件のコメント:
コメントを投稿